Để giải bài toán hình học liên quan đến tam giác và các đường vuông góc, chúng ta sẽ thực hiện các bước sau:

### Đề bài:
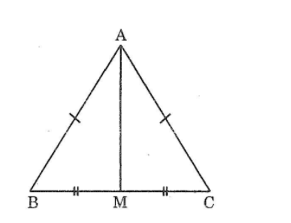
Cho tam giác \( ABC \) với \( AM \) vuông góc với \( BC \) tại \( M \), và \( CN \) vuông góc với \( AB \) tại \( N \).

#### a. Chứng minh \( BK \) vuông góc với \( AC \):

1. **Chứng minh \( \angle AMB = \angle ANC = 90^\circ \)**:
- Từ giả thiết, ta biết \( AM \perp BC \) tại \( M \) và \( CN \perp AB \) tại \( N \). Vậy \( \angle AMB \) và \( \angle ANC \) đều là góc vuông.

2. **Chứng minh \( AM = CN \)**:
- Để chứng minh điều này, ta sẽ sử dụng định lý Pythagoras hoặc các thuộc tính của hình chữ nhật.

3. **Chứng minh \( BK \perp AC \)**:
- Ta sẽ sử dụng các tính chất của tam giác vuông và đường cao để chứng minh. Ta có \( AM \) và \( CN \) đều là các đường vuông góc với các cạnh của tam giác, và \( BK \) là đường phân giác của góc \( \angle BAC \) trong tam giác vuông.

### b. Tính góc \( \angle MKN \) và góc \( \angle KBN \) khi \( MA = MB \) và \( \angle ABC = 55^\circ \):

1. **Tính \( \angle MKN \)**:
- Từ giả thiết \( MA = MB \), tam giác \( AMB \) là tam giác cân với \( AM \perp BC \) và \( MB \perp AC \), do đó \( \angle MBC = \angle MCB \).

- Để tính góc \( \angle MKN \), ta cần biết thêm thông tin về vị trí của \( K \). Nếu \( K \) là giao điểm của đường phân giác \( BK \) với \( AC \), ta có thể sử dụng tính chất của phân giác trong tam giác vuông.

2. **Tính \( \angle KBN \)**:
- Ta có \( \angle ABC = 55^\circ \). Trong tam giác vuông, góc \( \angle KBN \) có thể được tính dựa vào góc của tam giác vuông và góc của tam giác vuông cân.

### Tổng kết

- **Chứng minh**: Sử dụng các tính chất của tam giác vuông và các đường vuông góc.
- **Tính góc**: Dựa vào các định lý hình học và tính chất của góc trong tam giác vuông cân.

Các góc cụ thể \( \angle MKN \) và \( \angle KBN \) có thể cần thêm thông tin để tính toán chính xác. Để có đáp án chính xác hơn, cần biết vị trí của điểm \( K \) cụ thể.

Để giải bài toán hình học liên quan đến tam giác và các đường vuông góc, chúng ta sẽ thực hiện các bước sau:

### Đề bài:
Cho tam giác ABCABC với AMAM vuông góc với BCBC tại MM, và CNCN vuông góc với ABAB tại NN.

#### a. Chứng minh BKBK vuông góc với ACAC:

1. **Chứng minh ∠AMB=∠ANC=90∘∠AMB=∠ANC=90∘**:
- Từ giả thiết, ta biết AM⊥BCAM⊥BC tại MM và CN⊥ABCN⊥AB tại NN. Vậy ∠AMB∠AMB và ∠ANC∠ANC đều là góc vuông.

2. **Chứng minh AM=CNAM=CN**:
- Để chứng minh điều này, ta sẽ sử dụng định lý Pythagoras hoặc các thuộc tính của hình chữ nhật.

3. **Chứng minh BK⊥ACBK⊥AC**:
- Ta sẽ sử dụng các tính chất của tam giác vuông và đường cao để chứng minh. Ta có AMAM và CNCN đều là các đường vuông góc với các cạnh của tam giác, và BKBK là đường phân giác của góc ∠BAC∠BAC trong tam giác vuông.

### b. Tính góc ∠MKN∠MKN và góc ∠KBN∠KBN khi MA=MBMA=MB và ∠ABC=55∘∠ABC=55∘:

1. **Tính ∠MKN∠MKN**:
- Từ giả thiết MA=MBMA=MB, tam giác AMBAMB là tam giác cân với AM⊥BCAM⊥BC và MB⊥ACMB⊥AC, do đó ∠MBC=∠MCB∠MBC=∠MCB.

- Để tính góc ∠MKN∠MKN, ta cần biết thêm thông tin về vị trí của KK. Nếu KK là giao điểm của đường phân giác BKBK với ACAC, ta có thể sử dụng tính chất của phân giác trong tam giác vuông.

2. **Tính ∠KBN∠KBN**:
- Ta có ∠ABC=55∘∠ABC=55∘. Trong tam giác vuông, góc ∠KBN∠KBN có thể được tính dựa vào góc của tam giác vuông và góc của tam giác vuông cân.

### Tổng kết

- **Chứng minh**: Sử dụng các tính chất của tam giác vuông và các đường vuông góc.
- **Tính góc**: Dựa vào các định lý hình học và tính chất của góc trong tam giác vuông cân.

Các góc cụ thể ∠MKN∠MKN và ∠KBN∠KBN có thể cần thêm thông tin để tính toán chính xác. Để có đáp án chính xác hơn, cần biết vị trí của điểm KK cụ thể.