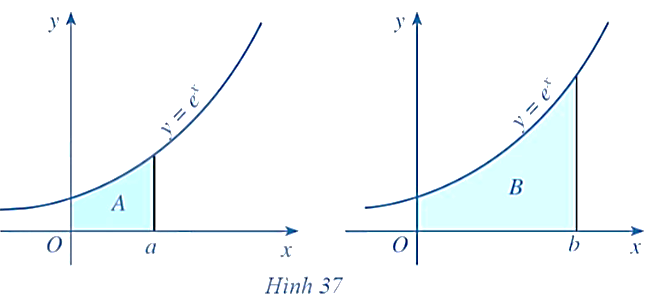
Giả sử A, B lần lượt là diện tích các hình được tô màu ở Hình 37.
Quảng cáo
2 câu trả lời 111
Tính diện tích \( A \) và \( B \)
Ta được cho hai diện tích \( A \) và \( B \) được định nghĩa như sau:
\[
A = \int_{0}^{a} e^x \, dx
\]
\[
B = \int_{0}^{b} e^x \, dx
\]
Tích phân của \( e^x \) theo \( x \) là \( e^x \), do đó ta có thể tính diện tích này như sau:
\[
A = e^x \Big|_0^a = e^a - e^0 = e^a - 1
\]
\[
B = e^x \Big|_0^b = e^b - e^0 = e^b - 1
\]
Giải pt \( B = 3A \)
Ta được cho phương trình:
\[
B = 3A
\]
Thay thế các biểu thức của \( A \) và \( B \) vào, ta có:
\[
e^b - 1 = 3(e^a - 1)
\]
giải phương trình để tìm \( b \):
\[
e^b - 1 = 3e^a - 3
\]
\[
e^b = 3e^a - 2
\]
\[
b = \ln(3e^a - 2)
\]
=>
\[
b = \ln(3e^a - 2)
\]
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272



