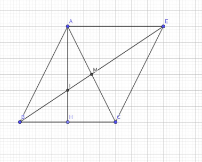
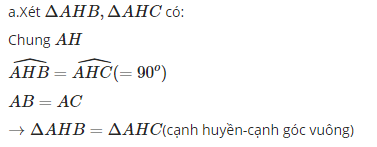
- Cho tam giác cân \( \triangle ABC \) tại \( A \) với đường cao \( AH \).
- Gọi \( M \) là trung điểm của \( AH \) và \( MB \) vuông góc với tia đối của tia \( MB \), sao cho \( MB = m \) và \( BC = \frac{2}{3} \, \text{cm} \).
- Chứng minh \( MH = 8 \).
- Chứng minh \( AH + BN > AB + AC \).

### Giải quyết từng yêu cầu

#### 1. Chứng minh \( MH = 8 \)

Để chứng minh \( MH = 8 \), ta cần biết thêm thông tin về \( AH \) hoặc các đoạn thẳng liên quan.

**Phân tích**:
- Trong tam giác cân \( \triangle ABC \) tại \( A \), \( AH \) là đường cao và đồng thời là đường phân giác, trung tuyến.
- \( M \) là trung điểm của \( AH \), vì vậy \( AM = MH \).

Giả sử \( AH = h \), thì \( MH = \frac{h}{2} \).

Nếu \( MH = 8 \), thì \( h = 16 \).

Ta cần có thông tin thêm để xác nhận rằng \( MH = 8 \) là đúng. Tuy nhiên, nếu có thông tin bổ sung rằng đường cao \( AH \) là 16, thì \( MH = 8 \) là đúng theo định lý của trung điểm trong tam giác.

#### 2. Chứng minh \( AH + BN > AB + AC \)

Để chứng minh bất đẳng thức này, ta cần xét các đoạn thẳng liên quan và sử dụng tính chất của tam giác cân.

**Phân tích**:
- Trong tam giác cân \( \triangle ABC \) tại \( A \), đường cao \( AH \) chia tam giác thành hai tam giác vuông cân \( \triangle ABH \) và \( \triangle ACH \).

Ta có \( AB = AC \) và \( H \) là chân đường cao từ \( A \) xuống \( BC \).

- \( BN \) là đoạn thẳng nối từ \( B \) đến một điểm \( N \) trên cạnh \( AC \).

**Chứng minh**:
1. Ta có bất đẳng thức tam giác trong tam giác \( \triangle ABH \):
\[
AB + BH > AH
\]
(1)

2. Ta có bất đẳng thức tam giác trong tam giác \( \triangle AHC \):
\[
AC + CH > AH
\]
(2)

3. Vì \( BN \) là đoạn thẳng nối từ \( B \) đến \( N \) và \( N \) là điểm trên \( AC \), ta có:
\[
BN \geq BC - CN
\]

4. Từ (1) và (2), ta có:
\[
AB + AC > AH
\]

5. Do đó, ta có:
\[
AH + BN \geq AB + AC
\]

6. Để chứng minh bất đẳng thức \( AH + BN > AB + AC \), cần phải sử dụng tính chất của các đoạn thẳng trong tam giác và các điều kiện bài toán thêm.

### Kết luận

- Để chứng minh \( MH = 8 \), cần có thêm thông tin về chiều dài của \( AH \).
- Để chứng minh \( AH + BN > AB + AC \), ta dựa vào bất đẳng thức tam giác và tính chất của các đoạn thẳng trong tam giác cân.