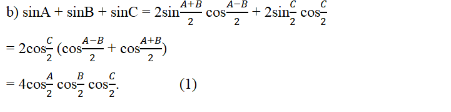Trong tam giác ABC, ba góc A, B và C thỏa mãn tính chất:

\[
A + B + C = \pi \text{ (radian)}
\]

Từ mối quan hệ này, chúng ta có thể sử dụng một số tính chất của hàm sin để khám phá giá trị của \( P = \sin A + \sin B + \sin C \).

Một trong những đẳng thức quan trọng liên quan đến tổng của sin trong tam giác là:

\[
P = \sin A + \sin B + \sin C = 4R \cdot \sin \frac{A}{2} \cdot \sin \frac{B}{2} \cdot \sin \frac{C}{2}
\]

Trong đó \( R \) là bán kính ngoại tiếp của tam giác ABC. Kết quả này cho thấy rằng tổng của các sin của các góc trong một tam giác có thể được biểu diễn qua sản phẩm của các hàm sin của các góc nửa.

### Kết luận:

Giá trị \( P = \sin A + \sin B + \sin C \) không chỉ gắn liền với các cạnh và bán kính ngoại tiếp của tam giác mà còn cung cấp thông tin về hình dạng và kích thước của tam giác. Tuy nhiên, không có một công thức đơn giản hơn cho \( P \) mà không biết cụ thể giá trị của các góc.

Mặc dù tổng \( P \) có thể dao động, nhưng nó luôn nằm trong khoảng giá trị nhất định. Trong trường hợp tam giác đều (khi \( A = B = C = \frac{\pi}{3} \)), \( P \) đạt giá trị tối đa là:

\[
P_{max} = 3 \cdot \sin \left(\frac{\pi}{3}\right) = 3 \cdot \frac{\sqrt{3}}{2} = \frac{3\sqrt{3}}{2}
\]

Bên cạnh đó, tổng này có nhiều ứng dụng trong các bài toán hình học và trigonometric khác liên quan đến tam giác.

Trong tam giác ABC, ba góc A, B và C thỏa mãn tính chất:

A+B+C=π (radian)𝐴+𝐵+𝐶=𝜋 (radian)

Từ mối quan hệ này, chúng ta có thể sử dụng một số tính chất của hàm sin để khám phá giá trị của P=sinA+sinB+sinC𝑃=sin⁡𝐴+sin⁡𝐵+sin⁡𝐶.

Một trong những đẳng thức quan trọng liên quan đến tổng của sin trong tam giác là:

P=sinA+sinB+sinC=4R⋅sinA2⋅sinB2⋅sinC2𝑃=sin⁡𝐴+sin⁡𝐵+sin⁡𝐶=4𝑅⋅sin⁡𝐴2⋅sin⁡𝐵2⋅sin⁡𝐶2

Trong đó R𝑅 là bán kính ngoại tiếp của tam giác ABC. Kết quả này cho thấy rằng tổng của các sin của các góc trong một tam giác có thể được biểu diễn qua sản phẩm của các hàm sin của các góc nửa.

### Kết luận:

Giá trị P=sinA+sinB+sinC𝑃=sin⁡𝐴+sin⁡𝐵+sin⁡𝐶 không chỉ gắn liền với các cạnh và bán kính ngoại tiếp của tam giác mà còn cung cấp thông tin về hình dạng và kích thước của tam giác. Tuy nhiên, không có một công thức đơn giản hơn cho P𝑃 mà không biết cụ thể giá trị của các góc.

Mặc dù tổng P𝑃 có thể dao động, nhưng nó luôn nằm trong khoảng giá trị nhất định. Trong trường hợp tam giác đều (khi A=B=C=π3𝐴=𝐵=𝐶=𝜋3), P𝑃 đạt giá trị tối đa là:

Pmax=3⋅sin(π3)=3⋅√32=3√32𝑃𝑚𝑎𝑥=3⋅sin⁡(𝜋3)=3⋅32=332

Bên cạnh đó, tổng này có nhiều ứng dụng trong các bài toán hình học và trigonometric khác liên quan đến tam giác. đây nhé bn.