Quảng cáo
1 câu trả lời 362
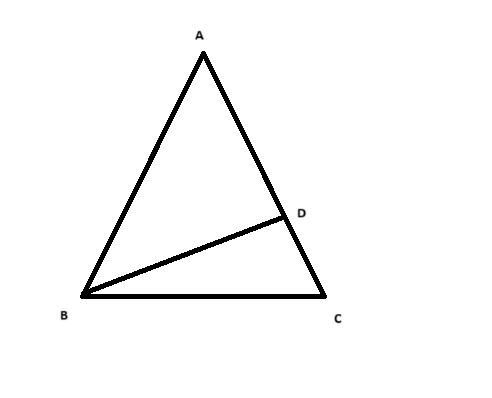
### Bước 1: Tính độ dài \( AD \)
Trong tam giác \( ABD \) và \( ACD \), ta có:
\[
AB^2 = AD^2 + BD^2
\]
\[
AC^2 = AD^2 + BD^2
\]
Vì \( AB = AC \) nên:
\[
AB^2 = AC^2
\]
Vậy:
\[
AD^2 + BD^2 = AB^2
\]
Thay giá trị \( AB = 17 \text{ cm} \) và \( BD = 15 \text{ cm} \) vào:
\[
AD^2 + 15^2 = 17^2
\]
\[
AD^2 + 225 = 289
\]
\[
AD^2 = 289 - 225
\]
\[
AD^2 = 64
\]
\[
AD = \sqrt{64} = 8 \text{ cm}
\]
### Bước 2: Tính cạnh \( BC \)
Vì \( D \) là trung điểm của \( BC \) trong tam giác cân tại \( A \) (do \( BD \) vuông góc với \( AC \)), ta có thể tính độ dài \( BC \) bằng cách sử dụng định lý Pythagoras trong tam giác \( BDC \) (lưu ý: \( D \) là trung điểm nên \( BD \) là đoạn phân giác của góc vuông \( BDC \)).
Trong tam giác vuông \( BDC \):
\[
BC^2 = BD^2 + DC^2
\]
Vì \( BD \) là đoạn vuông góc từ \( B \) đến \( AC \), nên trong tam giác vuông \( BDC \), \( DC \) chính là \( AD \) trong tam giác cân này.
Vậy:
\[
BC = 2 \times BD = 2 \times 15 = 30 \text{ cm}
\]
**Tóm lại:**
Cạnh \( BC \) có độ dài là \( 30 \text{ cm} \).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107593
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68300
Đã trả lời bởi chuyên gia
68300 -
 Đã trả lời bởi chuyên gia
52884
Đã trả lời bởi chuyên gia
52884 -
 Đã trả lời bởi chuyên gia
47390
Đã trả lời bởi chuyên gia
47390 -
 Đã trả lời bởi chuyên gia
45461
Đã trả lời bởi chuyên gia
45461 -
 Đã trả lời bởi chuyên gia
45109
Đã trả lời bởi chuyên gia
45109 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38488
Đã trả lời bởi chuyên gia
38488 -
 Đã trả lời bởi chuyên gia
38230
Đã trả lời bởi chuyên gia
38230


