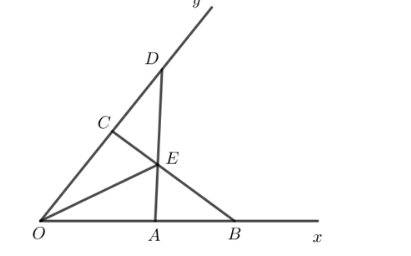
Để giải các bài toán liên quan đến tam giác và phân giác trong mặt phẳng tọa độ, ta sẽ sử dụng các tính chất hình học cơ bản. Dưới đây là các chứng minh cho từng câu hỏi:

### Cho dữ liệu:
- Góc \( xOy = 90^\circ \).
- \( A, B \) thuộc tia \( Ox \) sao cho \( OA < OB \).
- \( C, D \) thuộc tia \( Oy \) sao cho \( OC = OA \) và \( OD = OB \).
- \( E \) là giao điểm của \( AD \) và \( BC \).

### a. Chứng minh \( \triangle OBC \cong \triangle ODA \)

Để chứng minh hai tam giác \( \triangle OBC \) và \( \triangle ODA \) bằng nhau, ta sẽ sử dụng các cạnh và góc của tam giác:

1. **Cạnh bằng nhau:**
- \( OB = OD \) (Theo dữ liệu, vì \( OD = OB \)).
- \( OA = OC \) (Theo dữ liệu, vì \( OC = OA \)).

2. **Góc vuông:**
- Góc \( O \) trong cả hai tam giác đều bằng \( 90^\circ \) vì \( xOy = 90^\circ \).

3. **Góc giữa các cạnh:**
- Góc \( \angle OBC \) và \( \angle ODA \) đều bằng \( 90^\circ \), vì chúng là các góc vuông.

Vì vậy, theo tiêu chí góc-cạnh-góc (RHS), ta có:
\[
\triangle OBC \cong \triangle ODA
\]

### b. Chứng minh \( \triangle DBC \cong \triangle ODA \)

Để chứng minh hai tam giác \( \triangle DBC \) và \( \triangle ODA \) bằng nhau, ta sử dụng các cạnh và góc sau:

1. **Cạnh bằng nhau:**
- \( OD = OB \) (Theo dữ liệu).
- \( OA = OC \) (Theo dữ liệu).
- \( \triangle ODA \cong \triangle OBC \) từ phần (a), do đó \( OD = OB \) và \( OA = OC \).

2. **Góc vuông:**
- Góc \( \angle DBC \) và \( \angle ODA \) đều là góc vuông (90°).

3. **Cạnh \( DB \) và \( DA \) trong các tam giác tương ứng đều bằng nhau vì chúng là các đoạn thẳng nối hai điểm trên các tia đối diện nhau.

Từ các thông tin này, ta có:
\[
\triangle DBC \cong \triangle ODA
\]

### c. Chứng minh \( EB = ED \)

Để chứng minh rằng \( EB = ED \), ta sử dụng tính chất của các tam giác đồng dạng và các điểm đặc biệt:

1. **Tam giác đồng dạng:**
- Từ phần (b), ta đã chứng minh rằng \( \triangle DBC \cong \triangle ODA \).
- Vì vậy, các đoạn \( EB \) và \( ED \) phải bằng nhau vì \( E \) là giao điểm của \( AD \) và \( BC \).

2. **Chứng minh cụ thể:**
- Ta thấy rằng điểm \( E \) là giao điểm của \( AD \) và \( BC \) trong các tam giác đồng dạng.
- Do đó, khoảng cách từ \( E \) đến các điểm tương ứng \( B \) và \( D \) phải bằng nhau theo định lý về tam giác đồng dạng.

Vì vậy:
\[
EB = ED
\]

### d. Chứng minh \( OE \) là tia phân giác của \( xOy \)

Để chứng minh rằng \( OE \) là tia phân giác của góc \( xOy \):

1. **Tam giác đồng dạng:**
- Ta đã chứng minh rằng \( \triangle OBC \cong \triangle ODA \), và \( \triangle DBC \cong \triangle ODA \).
- Trong các tam giác này, \( OE \) chia các góc thành hai phần bằng nhau.

2. **Góc phân giác:**
- Tia phân giác của góc sẽ chia góc thành hai góc bằng nhau. Vì vậy, từ các tam giác đồng dạng đã chứng minh, ta có thể suy luận rằng \( OE \) là tia phân giác của \( xOy \).

Do đó, \( OE \) chia góc \( xOy \) thành hai góc bằng nhau.

### Kết luận:
- **a.** \( \triangle OBC \cong \triangle ODA \)
- **b.** \( \triangle DBC \cong \triangle ODA \)
- **c.** \( EB = ED \)
- **d.** \( OE \) là tia phân giác của \( xOy \)