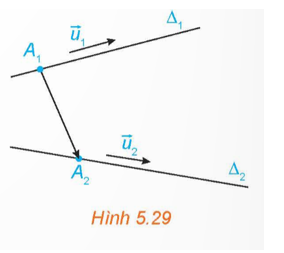
Trong không gian Oxyz, cho hai đường thẳng D1; D2 lần lượt đi qua các điểm A1(x1; y1; z1), A2(x2; y2; z2) và tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\) (H.5.29).
a) Tìm điều kiện đối với \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) để D1 và D2 song song hoặc trùng nhau.
b) Giả sử \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \) và \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\) thì D1 và D2 có cắt nhau hay không?
c) Giả sử \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\) thì D1 và D2 có chéo nhau hay không?
Quảng cáo
1 câu trả lời 64
a) D1 // D2 \( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{u_1}} = k\overrightarrow {{u_2}} \\{A_1} \notin {\Delta _2}\end{array} \right.\).
D1 ≡ D2 \( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{u_1}} = k\overrightarrow {{u_2}} \\{A_1} \in {\Delta _2}\end{array} \right.\).
b) D1 và D2 cắt nhau khi và chỉ khi \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \)không cùng phương và \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{A_1}{A_2}} \) đồng phẳng. Tức là \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \) và \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\).
c) D1 và D2 chéo nhau khi và chỉ khi \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{A_1}{A_2}} \) không đồng phẳng. Tức là: \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129704
Đã trả lời bởi chuyên gia
129704 -
 Đã trả lời bởi chuyên gia
104155
Đã trả lời bởi chuyên gia
104155 -
 Đã trả lời bởi chuyên gia
94109
Đã trả lời bởi chuyên gia
94109 -
 Đã trả lời bởi chuyên gia
69540
Đã trả lời bởi chuyên gia
69540



