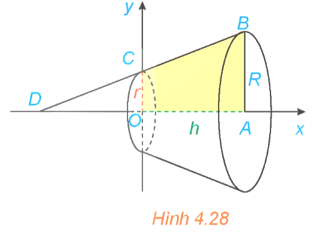
a) Tính thể tích của khối tròn xoay sinh ra khi quay hình thang vuông OABC trong mặt phẳng Oxy với OA = h, AB = R và OC = r, quanh trục Ox (H.4.28).
b) Từ công thức thu được ở phần a, hãy rút ra công thức tính thể tích của khối nón có bán kính đáy bằng R và chiều cao h.
Quảng cáo
1 câu trả lời 133
a) Chọn hệ trục như hình vẽ.
Khi đó ta có C(0; r), B(h; R). Suy ra \(\overrightarrow {BC} = \left( {h;R - r} \right)\).
Phương trình đường thẳng BC qua C và nhận \(\overrightarrow n = \left( {r - R;h} \right)\) có dạng:
(r – R)x + h(y − r) = 0 hay \[y = \frac{{hr + \left( {R - r} \right)x}}{h}\].
Thể tích cần tính là:
\(V = \pi {\int\limits_0^h {\left[ {\frac{{hr + \left( {R - r} \right)x}}{h}} \right]} ^2}dx\)\( = \pi \int\limits_0^h {\left[ {{r^2} + 2r.\frac{{R - r}}{h}x + {{\left( {\frac{{R - r}}{h}x} \right)}^2}} \right]} dx\)
\( = \pi \left. {\left( {{r^2}x + r.\frac{{R - r}}{h}.{x^2} + {{\left( {\frac{{R - r}}{h}} \right)}^2}.\frac{{{x^3}}}{3}} \right)} \right|_0^h\)\( = \pi \left[ {{r^2}h + \left( {Rr - {r^2}} \right).h + \frac{{{{\left( {R - r} \right)}^2}.h}}{3}} \right]\)
\( = \pi \left( {{r^2}h + Rrh - {r^2}h + \frac{1}{3}{R^2}h - \frac{2}{3}Rrh + \frac{1}{3}{r^2}h} \right)\)\( = \pi \left( {\frac{1}{3}{R^2}h + \frac{1}{3}Rrh + \frac{1}{3}{r^2}h} \right)\)
\[ = \frac{1}{3}\pi h\left( {{R^2} + Rr + {r^2}} \right)\].
b) Khi r = 0 thì khối nón cụt trở thành khối nón có chiều cao h, bán kính đáy là R.
Do đó \(V = \frac{1}{3}\pi {R^2}h\).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129704
Đã trả lời bởi chuyên gia
129704 -
 Đã trả lời bởi chuyên gia
104155
Đã trả lời bởi chuyên gia
104155 -
 Đã trả lời bởi chuyên gia
94109
Đã trả lời bởi chuyên gia
94109 -
 Đã trả lời bởi chuyên gia
69540
Đã trả lời bởi chuyên gia
69540



