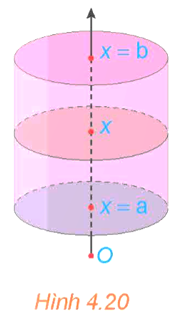
Xét hình trụ có bán kính đáy R, có trục là trục hoành Ox, nằm giữa hai mặt phẳng x = a và x = b (a < b) (H.4.20).
a) Tính thể tích V của hình trụ.
b) Tính diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x (a ≤ x ≤ b). Từ đó tính và so sánh với V.
Quảng cáo
1 câu trả lời 77
a) Độ dài chiều cao hình trụ là: h = b – a.
Thể tích của hình trụ là: V = πR2h = πR2(b – a).
b) Diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox là
S(x) = πR2.
Ta có \(\int\limits_a^b {S\left( x \right)} dx\)\[ = \int\limits_a^b {\pi {R^2}} dx\]\[ = \left. {\left( {\pi {R^2}x} \right)} \right|_a^b\]\[ = \pi {R^2}\left( {b - a} \right)\].
Vậy \(V = \int\limits_a^b {S\left( x \right)} dx\).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129704
Đã trả lời bởi chuyên gia
129704 -
 Đã trả lời bởi chuyên gia
104155
Đã trả lời bởi chuyên gia
104155 -
 Đã trả lời bởi chuyên gia
94109
Đã trả lời bởi chuyên gia
94109 -
 Đã trả lời bởi chuyên gia
69540
Đã trả lời bởi chuyên gia
69540



