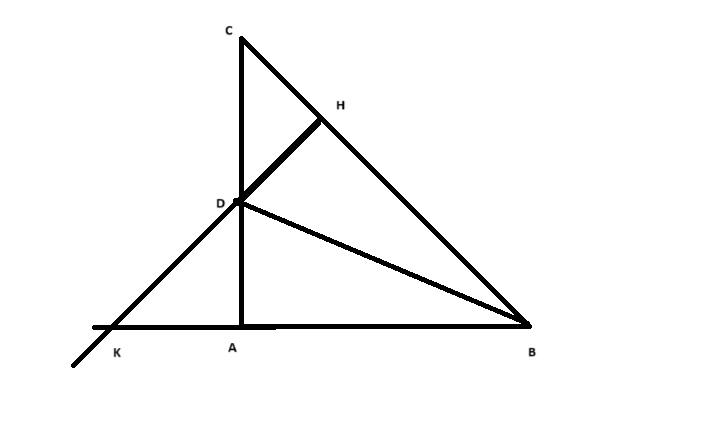
Trong tam giác \(ABC\) vuông tại \(A\) (với \(AB < AC\)), ta có \(BD\) là tia phân giác của góc \(B\), \(D\) là điểm thuộc \(AC\). Kẻ \(DH \perp BC\) tại \(H\), kéo dài \(DH\) cắt tia \(BA\) tại \(K\). Để chứng minh tam giác \(DHC\) đồng dạng với tam giác \(DAK\), ta sẽ xem xét các góc tương ứng và sử dụng các tính chất của tam giác vuông, phân giác, và các góc vuông.

1. Chứng minh tam giác \(DHC\) ~ tam giác \(DAK\)

Xét các góc trong tam giác:

1. Góc \(\angle DHC\) và \(\angle DAK\):
- \(\angle DHC = 90^\circ\) (do \(DH \perp BC\)).
- \(\angle DAK = 90^\circ\) (do \(AK\) là đường cao của tam giác vuông \(ABK\) tại \(K\)).

Vậy, ta có \(\angle DHC = \angle DAK = 90^\circ\).

2. Góc \(\angle CDH\) và \(\angle KDA\):
- Vì \(BD\) là phân giác của góc \(B\) trong tam giác vuông \(ABC\), nên \(\angle ABD = \angle CBD\).
- Trong tam giác \(DHC\), góc \(C\) và góc \(H\) đối đỉnh với nhau, nên \(\angle CDH = \angle BDH\).
- Trong tam giác \(DAK\), góc \(A\) và góc \(K\) đối đỉnh với nhau, nên \(\angle KDA = \angle BDA\).

Từ tính chất tia phân giác và các góc đối đỉnh, ta có:
- \(\angle CDH = \angle ABD\)
- \(\angle KDA = \angle BDA\)

3. Góc \(\angle BDA\) và \(\angle BDH\):
- Cả hai góc \(\angle BDA\) và \(\angle BDH\) đều nằm trong tam giác vuông \(BDA\), với \(\angle BDA\) và \(\angle BDH\) đều bằng nhau (vì chúng cùng bằng nửa góc \(B\) trong tam giác vuông \(ABC\)).

Như vậy, ta có ba cặp góc bằng nhau giữa tam giác \(DHC\) và tam giác \(DAK\):

- \(\angle DHC = \angle DAK = 90^\circ\)
- \(\angle CDH = \angle KDA\)
- \(\angle HDC = \angle AKD\) (do tính chất các góc đối đỉnh và góc trong tam giác vuông)

Từ đó, theo định lý đồng dạng về góc-góc (AA), ta kết luận:

Tam giác \(DHC\) đồng dạng với tam giác \(DAK\).