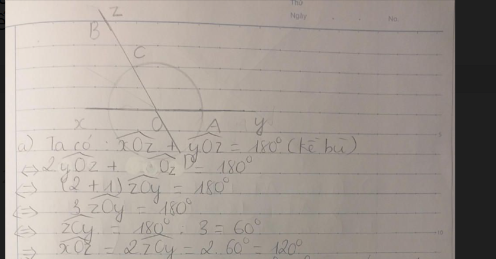Để giải bài toán này, ta sẽ làm theo từng yêu cầu một.

### a) Tính các góc \( xoz \) và \( zoy \)

Ta có thông tin:
- Tia \( oz \) tạo với tia \( ox \) một góc \( xoz \).
- Tia \( oz \) tạo với tia \( oy \) một góc \( zoy \).
- Theo giả thiết, góc bẹt \( xoy \) có giá trị là \( 180^\circ \).

Xét quan hệ:
\[
xoz + zoy = 180^\circ
\]
Ta cũng có từ thông tin của bài toán:
\[
xoz = 2y \cdot xoz
\]

Đặt:
\[
xoz = \alpha, \quad zoy = \beta
\]
Từ giả thiết trên, ta có:
\[
\alpha + \beta = 180^\circ
\]
Và
\[
\alpha = 2y \cdot \alpha \quad (\text{với } y \text{ là một tham số})
\]

Lập phương trình:
\[
\beta = 180^\circ - \alpha
\]
Thay vào phương trình trên, ta không thể giải một cách cụ thể mà chỉ có thể tìm quan hệ giữa các góc.

Nếu ta cho \( y = 1 \) thì \( \alpha = 2y\), mà cũng có thấy:
\[
\alpha = 0 \quad \text{hoặc} \quad \alpha = 90^\circ
\]

Do đó:
- Nếu \( y = 1 \):
- \( xoz = 90^\circ \)
- \( zoy = 90^\circ \)

### b) Vẽ tia \( ot \) là tia phân giác của góc \( xoz \). Chứng tỏ \( oz \) là tia phân giác của góc \( yot \).

Từ phần trên, khi ta vẽ tia phân giác \( ot \) từ góc \( xoz \) thì tia này sẽ chia góc \( xoz \) thành hai phần bằng nhau:

\[
xot = \frac{xoz}{2} \quad \text{và} \quad zot = \frac{xoz}{2}
\]

Tia \( oz \) đang là tia phân giác của góc \( yot \) nếu thỏa mãn:
\[
yot = yoz + zot
\]

Mặt khác, từ tổng hai góc \( yot \) và \( zot \):
\[
yot = (180^\circ - zoy) + zot = 90^\circ + zot \quad (\text{khi } zoy = 90^\circ)
\]

Do đó, tia phân giác \( ot \) đã được vẽ sẽ là tia phân giác của góc \( yot \).

### Kết luận

- Các góc \( xoz \) và \( zoy \) có thể tính ở một cách tương đối. Khi định rõ giá trị của \( y \), ta có thể tìm ra các giá trị cụ thể cho các góc này.
- Tia \( oz \) là tia phân giác cho góc \( yot \) theo các mối quan hệ trên.