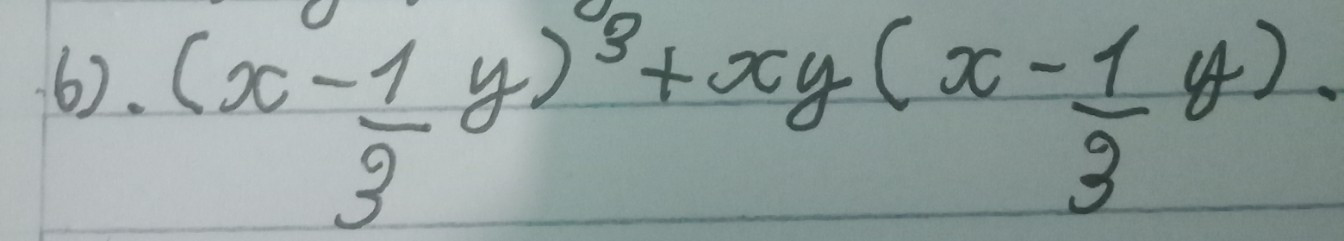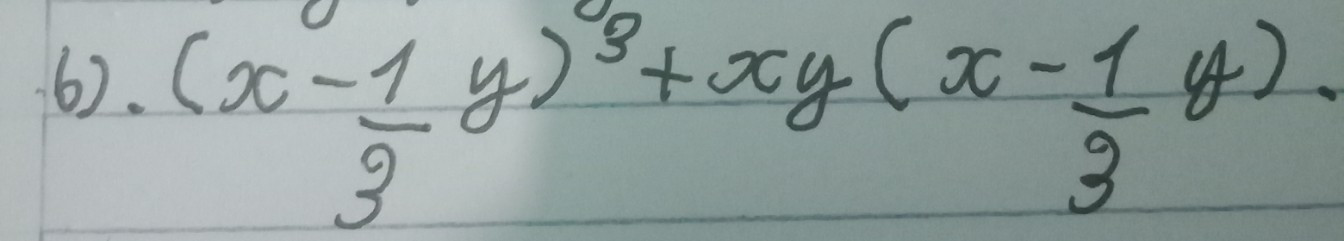Nguyễn Nguyễn Hồng Nhung
Hỏi từ APP VIETJACK
Giải bài tập toán rút gọn các biểu thức sau
Quảng cáo
3 câu trả lời 194
1 năm trước
Để rút gọn biểu thức \( b) \left(\frac{x - 1}{y}\right)^3 + \frac{xy (x - 1)}{y^3} \), ta thực hiện các bước sau:
1. Viết lại biểu thức ban đầu:
\[ b) \left(\frac{x - 1}{y}\right)^3 + \frac{xy (x - 1)}{y^3} \]
2. Rút gọn từng phần của biểu thức:
Biểu thức đầu tiên:
\[ \left(\frac{x - 1}{y}\right)^3 = \frac{(x - 1)^3}{y^3} \]
Biểu thức thứ hai:
\[ \frac{xy (x - 1)}{y^3} = \frac{(x - 1)xy}{y^3} = \frac{x(x - 1)}{y^2} \]
3. Kết hợp lại:
\[ \frac{(x - 1)^3}{y^3} + \frac{x(x - 1)}{y^3} \]
4. Quy đồng mẫu số:
\[ \frac{(x - 1)^3}{y^3} + \frac{x(x - 1)}{y^2} = \frac{(x - 1)^3 + xy(x - 1)}{y^3} \]
5. Đưa các biểu thức có cùng \(x-1\) ra ngoài:
\[ \frac{(x - 1)^2(x - 1) + x(x - 1)}{y^3} = \frac{(x - 1)^2(x - 1 + x)}{y^3} = \frac{(x - 1)^2(x + x - 1)}{y^3} = \frac{(x - 1)^2(2x - 1)}{y^3} \]
Vậy biểu thức rút gọn là:
\[ \boxed{\frac{(x - 1)^2(2x - 1)}{y^3}} \]
1. Viết lại biểu thức ban đầu:
\[ b) \left(\frac{x - 1}{y}\right)^3 + \frac{xy (x - 1)}{y^3} \]
2. Rút gọn từng phần của biểu thức:
Biểu thức đầu tiên:
\[ \left(\frac{x - 1}{y}\right)^3 = \frac{(x - 1)^3}{y^3} \]
Biểu thức thứ hai:
\[ \frac{xy (x - 1)}{y^3} = \frac{(x - 1)xy}{y^3} = \frac{x(x - 1)}{y^2} \]
3. Kết hợp lại:
\[ \frac{(x - 1)^3}{y^3} + \frac{x(x - 1)}{y^3} \]
4. Quy đồng mẫu số:
\[ \frac{(x - 1)^3}{y^3} + \frac{x(x - 1)}{y^2} = \frac{(x - 1)^3 + xy(x - 1)}{y^3} \]
5. Đưa các biểu thức có cùng \(x-1\) ra ngoài:
\[ \frac{(x - 1)^2(x - 1) + x(x - 1)}{y^3} = \frac{(x - 1)^2(x - 1 + x)}{y^3} = \frac{(x - 1)^2(x + x - 1)}{y^3} = \frac{(x - 1)^2(2x - 1)}{y^3} \]
Vậy biểu thức rút gọn là:
\[ \boxed{\frac{(x - 1)^2(2x - 1)}{y^3}} \]
Quảng cáo
Bạn hỏi - Chuyên gia trả lời
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
Đã trả lời bởi chuyên gia
68061 -
Đã trả lời bởi chuyên gia
52846
-
Đã trả lời bởi chuyên gia
47344
-
Đã trả lời bởi chuyên gia
45400
-
Đã trả lời bởi chuyên gia
45045
-
Hỏi từ APP VIETJACK
Đã trả lời bởi chuyên gia
38412
-
Đã trả lời bởi chuyên gia
38191
Thành viên hăng hái nhất trong tuần
-
보고 싶어요😢
1815 điểm
-
𝘳𝘺𝘯.𝘭𝘦𝘦ッ
305 điểm
-
우옌 ✨
170 điểm
-
Nguyễn Minh Kiệt
45 điểm
-
Kim Dan 20 điểm
-
Ngọc Nguyễn 20 điểm
-
Yanny 20 điểm
-
Mai Nguyễn Thị Thu 20 điểm
-
nhuu ye 20 điểm
-
Linh Nguyễn 20 điểm
-
Bacy Sam 20 điểm
-
Thảo vy Lê 20 điểm
-
Hong Bui 20 điểm
-
Ngluyn Hii 20 điểm
Rút gọn
Bài viết mới nhất Lớp 8
-
3 năm trước8253
-
3 năm trước7766
-
3 năm trước6589
-
3 năm trước6480
-
3 năm trước6306
Gửi báo cáo thành công!
