Quảng cáo
2 câu trả lời 189
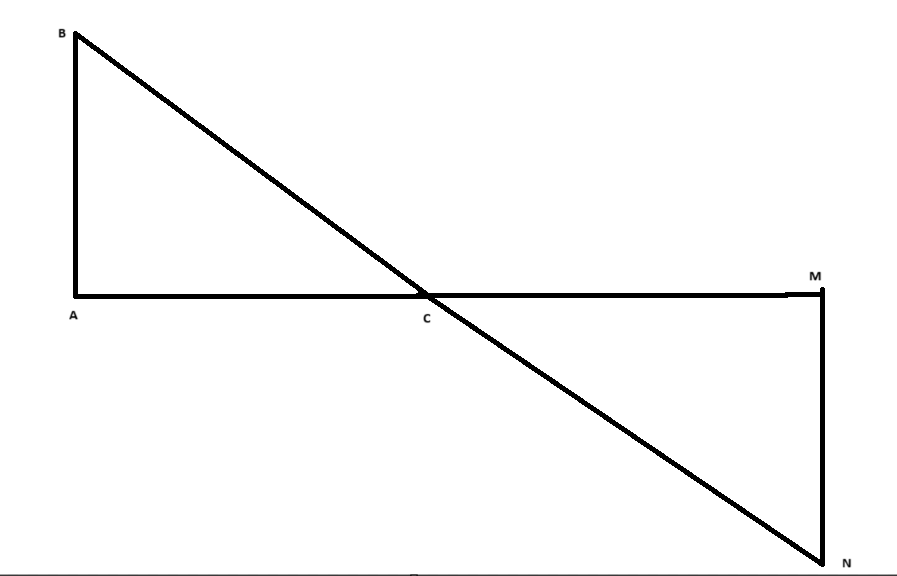
1. **Xác định các điểm trung điểm**:
- \(C\) là trung điểm của \(AM\), nên \(AC = CM\).
- \(C\) là trung điểm của \(BN\), nên \(BC = CN\).
2. **Xét các cặp cạnh tương ứng**:
- Ta có: \(AC = CM\) (do \(C\) là trung điểm của \(AM\))
- Ta có: \(BC = CN\) (do \(C\) là trung điểm của \(BN\))
- Ta cần chứng minh \(AB = MN\).
3. **Tính chất của tam giác vuông**:
- Trong tam giác \(ABC\), \( \angle BAC = 90^\circ\).
- Vì \(C\) là trung điểm của \(AM\), ta có \(\triangle ACM\) là tam giác vuông tại \(C\), với \(AC = CM\).
- Vì \(C\) là trung điểm của \(BN\), ta có \(\triangle BCN\) là tam giác vuông tại \(C\), với \(BC = CN\).
4. **Tính chất tam giác vuông tại các điểm trung điểm**:
- Vì \(AC = CM\) và \(BC = CN\), chúng ta cần chứng minh rằng \(AB = MN\).
- Chúng ta sẽ sử dụng định lý Pythagoras trong các tam giác vuông.
5. **Sử dụng định lý Pythagoras**:
- Trong tam giác vuông \(ABC\) tại \(A\):
\[
AB^2 = AC^2 + BC^2
\]
- Trong tam giác vuông \(MNC\):
\[
MN^2 = MC^2 + CN^2
\]
6. **So sánh các cặp cạnh**:
- Ta có: \(MC = AC\) và \(CN = BC\), vì \(C\) là trung điểm.
- Do đó:
\[
MN^2 = MC^2 + CN^2 = AC^2 + BC^2
\]
- Vì vậy:
\[
MN^2 = AB^2
\]
- Do đó: \(MN = AB\) và \( \triangle ABC \cong \triangle MNC \).
### Kết luận
Ta đã chứng minh rằng các cặp cạnh tương ứng và góc tương ứng của hai tam giác \(\triangle ABC\) và \(\triangle MNC\) bằng nhau, từ đó suy ra \(\triangle ABC \cong \triangle MNC\).
Vậy, △ABC=△MNC\triangle ABC = \triangle MNC△ABC=△MNC theo trường hợp cạnh-góc-cạnh (SAS).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


