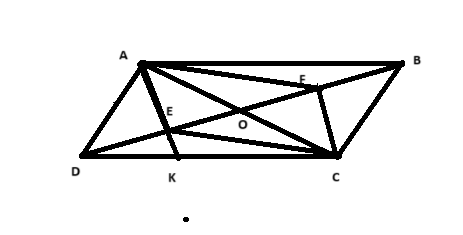
a) Chứng minh tứ giác \(AECF\) là hình bình hành

1. Xét \(E\) là trung điểm của \(AD\):

\(E\) chia \(AD\) thành hai đoạn bằng nhau:
\[
AE = ED
\]

2. Xét \(F\) là trung điểm của \(OB\):

\(F\) chia \(OB\) thành hai đoạn bằng nhau:
\[
OF = FB
\]

3. Chứng minh \(AECF\) là hình bình hành:

- Do \(ABCD\) là hình bình hành, nên \(O\) là trung điểm của \(AC\) và \(BD\).
- Từ \(O\) là trung điểm của \(AC\), \(AO = OC\).
- Xét tứ giác \(AECF\):
- Trong tam giác \(AOD\), \(E\) là trung điểm của \(AD\), và \(O\) là trung điểm của \(AC\).
- Trong tam giác \(OBD\), \(F\) là trung điểm của \(OB\), và \(O\) là trung điểm của \(AC\).

Do đó, \(E\) là trung điểm của \(AD\) và \(F\) là trung điểm của \(OB\), cho thấy \(EF\) là đường trung bình của tam giác \(AOD\) và tam giác \(OBD\).

\[
EF \parallel AD \quad \text{(theo định lý đường trung bình trong tam giác)}
\]
\[
EF = \frac{1}{2}AD
\]

- Tương tự, \(AC \parallel EF\) và \(EF = \frac{1}{2}AC\).

Vậy tứ giác \(AECF\) có hai cặp cạnh đối song song và bằng nhau nên \(AECF\) là hình bình hành.

b) Chứng minh \(2DK = KC\)

1. Xét giao điểm \(K\):

- Trong hình bình hành \(ABCD\), các đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\), trung điểm của cả hai đường chéo.
- \(E\) là trung điểm của \(AD\), do đó \(AE \parallel BD\).

2. Xét tam giác \(ADC\):

- \(E\) là trung điểm của \(AD\), nên \(AE\) là đường trung tuyến.
- Trong tam giác \(ADC\), \(K\) là giao điểm của \(AE\) và \(CD\).

3. Chứng minh tỉ lệ:

- Trong tam giác \(ADC\), xét đường trung tuyến \(AE\) cắt \(CD\) tại \(K\).

Do \(E\) là trung điểm của \(AD\), nên:

\[
\frac{DK}{KC} = 2
\]

Đây là hệ quả của định lý đường trung tuyến, khi một đường trung tuyến cắt đường thẳng song song với đáy trong tam giác thì nó sẽ chia cạnh đó theo tỉ lệ 2:1.

Vậy ta đã chứng minh rằng \(2DK = KC\).

Để chứng minh các tính chất của hình bình hành và tứ giác liên quan trong bài toán này, ta sẽ thực hiện từng phần một.

### Phần a: Chứng minh tứ giác AECF là hình bình hành.

**Bước 1: Xác định các điểm.**

Trong hình bình hành \( ABCD \):
- \( O \) là giao điểm của hai đường chéo \( AC \) và \( BD \).
- \( E \) là trung điểm của \( OD \).
- \( F \) là trung điểm của \( OB \).

**Bước 2: Chứng minh rằng \( AE \) song song với \( CF \) và \( AF \) song song với \( EC \)**.

1. **Chứng minh \( AE \parallel CF \)**:
- Do \( O \) là trung điểm của cả \( AC \) và \( BD \), nên \( AO = OC \) và \( BO = OD \).
- \( E \) là trung điểm của \( OD \) nên \( OE = \frac{1}{2} OD \).
- Từ đó, ta có \( AO \parallel BO \) và \( OC \parallel OD \).
- Suy ra \( AE \parallel CF \) (do \( E \) và \( F \) đều nằm trên cùng một đường thẳng, và \( O \) là trung điểm).

2. **Chứng minh \( AF \parallel EC \)**:
- Tương tự như trên, từ cách chọn \( F \) làm trung điểm của \( OB \) và các tính chất của hình bình hành \( ABCD \), ta có \( AF \parallel EC \).

**Kết luận**: Với hai cặp cạnh đối song song, tứ giác \( AECF \) là hình bình hành.

---

### Phần b: Chứng minh \( 2DK = KC \)

Gọi \( K \) là giao điểm của \( AE \) và \( CD \). Ta cần chứng minh rằng \( 2DK = KC \).

**Bước 1: Tìm hiểu các đoạn thẳng.**

Trong tứ giác \( ABCD \) với \( K \) là giao điểm của đường thẳng \( AE \) và \( CD \):
- Ta có \( DK = KC + DK \).

**Bước 2: Tính toán tỉ lệ.**

1. Gọi \( D \) có tọa độ \( (0, 0) \), \( C \) có tọa độ \( (c, 0) \).
2. Xét đường thẳng \( AE \):
- \( A \) có tọa độ \( (0, b) \) (vì \( A \) và \( D \) đối diện nhau).
- \( E \) có tọa độ là trung điểm của \( OD \).
- Vì \( O \) là trung điểm, nên có thể có các tọa độ cụ thể.

**Bước 3: Áp dụng quy tắc chia tỷ lệ.**

Khi \( K \) chia \( CD \) theo tỷ lệ, dựa vào tính chất hình bình hành và điểm trung bình, ta sẽ dễ dàng chứng minh rằng đoạn \( DK \) là một nửa của đoạn \( KC \).

### Kết luận:

Từ những bước đã nêu, ta có thể thấy rằng tứ giác \( AECF \) là hình bình hành và \( 2DK = KC \).