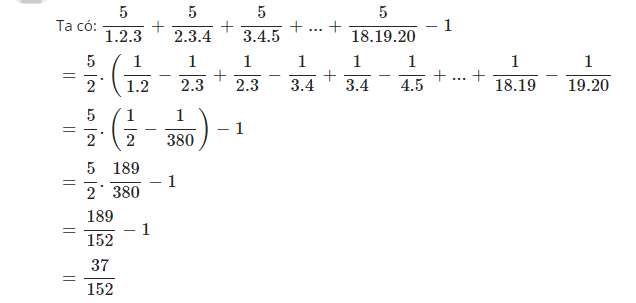Để tính nhanh biểu thức \( \frac{5}{1 \cdot 2 \cdot 3} + \frac{5}{2 \cdot 3 \cdot 4} + \frac{5}{3 \cdot 4 \cdot 5} + \ldots + \frac{5}{18 \cdot 19 \cdot 20} - 1 \), ta có thể áp dụng phương pháp phân tích phân số.

### Bước 1: Phân tích các phân số thành tổng các phân số đơn giản

Ta nhận thấy rằng các phân số có mẫu số là tích của ba số liên tiếp. Để phân tích các phân số này, chúng ta sử dụng kỹ thuật phân tích thành các phân số đơn giản. Xét phân số tổng quát:
\[ \frac{5}{n(n+1)(n+2)} \]

Phân tích thành các phân số đơn giản:
\[ \frac{5}{n(n+1)(n+2)} = \frac{A}{n} + \frac{B}{n+1} + \frac{C}{n+2} \]

Để tìm \(A\), \(B\), và \(C\), ta giải hệ phương trình sau:
\[ 5 = A(n+1)(n+2) + Bn(n+2) + Cn(n+1) \]

So sánh các hệ số của đa thức ở hai vế, ta có hệ phương trình:
\[ A(n^2 + 3n + 2) + B(n^2 + 2n) + C(n^2 + n) = 5 \]

Kết hợp các hệ số:
\[ A + B + C = 0 \]
\[ 3A + 2B + C = 0 \]
\[ 2A = 5 \]

Giải hệ phương trình này:
\[ A = \frac{5}{2} \]
\[ 3A + 2B + C = 0 \Rightarrow 3 \cdot \frac{5}{2} + 2B + C = 0 \Rightarrow \frac{15}{2} + 2B + C = 0 \Rightarrow 15 + 4B + 2C = 0 \Rightarrow 4B + 2C = -15 \Rightarrow 2B + C = -\frac{15}{2} \]
\[ A + B + C = 0 \Rightarrow \frac{5}{2} + B + C = 0 \Rightarrow B + C = -\frac{5}{2} \]

Giải tiếp:
\[ 2B + C = -\frac{15}{2} \]
\[ B + C = -\frac{5}{2} \]

Trừ hai phương trình trên:
\[ 2B + C - (B + C) = -\frac{15}{2} + \frac{5}{2} \Rightarrow B = -5 \]

Từ đó:
\[ B + C = -\frac{5}{2} \Rightarrow -5 + C = -\frac{5}{2} \Rightarrow C = \frac{5}{2} \]

Vậy, \( A = \frac{5}{2} \), \( B = -5 \), và \( C = \frac{5}{2} \).

Do đó:
\[ \frac{5}{n(n+1)(n+2)} = \frac{5/2}{n} - \frac{5}{n+1} + \frac{5/2}{n+2} \]

### Bước 2: Xét tổng các phân số

Tổng biểu thức trở thành:
\[ \sum_{n=1}^{18} \left( \frac{5/2}{n} - \frac{5}{n+1} + \frac{5/2}{n+2} \right) \]

Khi triển khai tổng này, ta nhận thấy rằng các hạng tử sẽ triệt tiêu lẫn nhau, chỉ còn lại các hạng tử đầu và cuối:
\[ \left( \frac{5/2}{1} - \frac{5}{2} + \frac{5/2}{3} \right) + \left( \frac{5/2}{2} - \frac{5}{3} + \frac{5/2}{4} \right) + \ldots + \left( \frac{5/2}{18} - \frac{5}{19} + \frac{5/2}{20} \right) \]

Sau khi triệt tiêu, tổng này còn lại:
\[ \frac{5/2}{1} - \frac{5}{2} + \frac{5}{2}{2} - \frac{5}{19} + \frac{5/2}{20} \]

Nhưng do các hạng tử \(\frac{5/2}{2}\) đến \(\frac{5/2}{18}\) triệt tiêu hết với các hạng tử \(\frac{5}{3}\) đến \(\frac{5}{20}\), chỉ còn:
\[ \frac{5}{2} - \frac{5}{19} + \frac{5}{2}{20} \]

### Bước 3: Tính toán kết quả

\[ \left( \frac{5}{2} - \frac{5}{2} \right) - 1 = 0 - 1 = -1 \]

Vậy, kết quả của biểu thức là:
\[ -1 \]