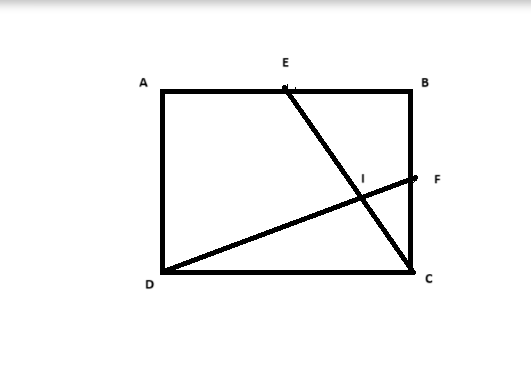
1. Giả sử hình vuông \(ABCD\) có cạnh dài \(a\). Các tọa độ của các đỉnh là:
- \(A(0,0)\)
- \(B(a,0)\)
- \(C(a,a)\)
- \(D(0,a)\)

2. Các điểm trung điểm \(E\) và \(F\) là:
- \(E\) là trung điểm của \(AB\) nên \(E\left(\frac{a}{2},0\right)\)
- \(F\) là trung điểm của \(BC\) nên \(F\left(a,\frac{a}{2}\right)\)

3. Xác định giao điểm \(I\) của \(DF\) và \(CE\):
- Đường thẳng \(DF\) đi qua \(D(0,a)\) và \(F(a,\frac{a}{2})\). Phương trình của \(DF\) là \(y = -\frac{1}{2}x + a\).
- Đường thẳng \(CE\) đi qua \(C(a,a)\) và \(E\left(\frac{a}{2},0\right)\). Phương trình của \(CE\) là \(y = 2x - a\).

Giao điểm \(I\) của hai đường thẳng \(DF\) và \(CE\) được tìm bằng cách giải hệ phương trình:
\[
\begin{cases}
y = -\frac{1}{2}x + a \\
y = 2x - a
\end{cases}
\]
Giải hệ phương trình này, ta có:
\[
-\frac{1}{2}x + a = 2x - a \\
a + a = 2x + \frac{1}{2}x \\
\frac{3a}{2} = \frac{5x}{2} \\
x = \frac{3a}{5} \\
y = 2\left(\frac{3a}{5}\right) - a = \frac{6a}{5} - a = \frac{a}{5}
\]
Vậy tọa độ điểm \(I\) là \(\left(\frac{3a}{5}, \frac{a}{5}\right)\).

4. Tính diện tích các tam giác \( \triangle CIE \) và \( \triangle CBE \):

Diện tích của một tam giác có tọa độ các đỉnh \((x_1, y_1), (x_2, y_2), (x_3, y_3)\) được tính bằng công thức:
\[
S = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|
\]

- Đối với tam giác \( \triangle CIE \):
\[
S_{CIE} = \frac{1}{2} \left| a \left( \frac{a}{5} - 0 \right) + \frac{3a}{5} \left( 0 - a \right) + \frac{a}{2} \left( a - \frac{a}{5} \right) \right|
\]
\[
S_{CIE} = \frac{1}{2} \left| a \cdot \frac{a}{5} - \frac{3a^2}{5} + \frac{a}{2} \cdot \frac{4a}{5} \right|
\]
\[
S_{CIE} = \frac{1}{2} \left| \frac{a^2}{5} - \frac{3a^2}{5} + \frac{2a^2}{5} \right| = \frac{1}{2} \left| \frac{a^2}{5} \right| = \frac{a^2}{10}
\]

- Đối với tam giác \( \triangle CBE \):
\[
S_{CBE} = \frac{1}{2} \left| a(0 - 0) + a(0 - a) + \frac{a}{2}(a - 0) \right|
\]
\[
S_{CBE} = \frac{1}{2} \left| 0 - a^2 + \frac{a^2}{2} \right| = \frac{1}{2} \left| -\frac{a^2}{2} \right| = \frac{a^2}{4}
\]

5. Tính tỉ số diện tích của \( \triangle CIE \) và \( \triangle CBE \):
\[
\text{Tỉ số} = \frac{S_{CIE}}{S_{CBE}} = \frac{\frac{a^2}{10}}{\frac{a^2}{4}} = \frac{4}{10} = \frac{2}{5}
\]

Vậy tỉ số diện tích của \( \triangle CIE \) và \( \triangle CBE \) là \(\boxed{\frac{2}{5}}\).