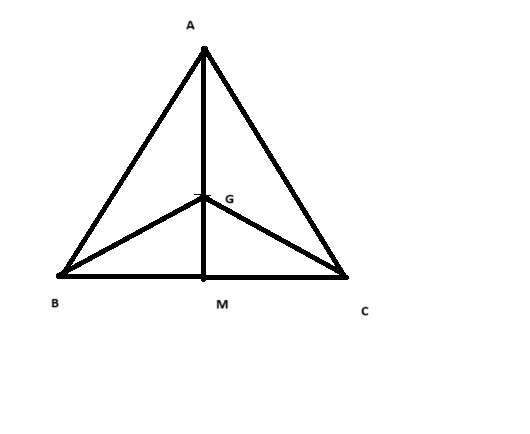
Để giải bài toán này, ta cần sử dụng các tính chất của tam giác đều và vectơ.

1. Tam giác ABC đều và trọng tâm G:
- Trọng tâm G của tam giác đều là điểm trùng điểm giao của các đường trung tuyến của tam giác, và là trọng tâm của tam giác (nghĩa là nó chia các đoạn thẳng từ các đỉnh đến các đoạn thẳng trung tuyến theo tỉ lệ 2:1).

2. M là trung điểm của BC:
- Vì M là trung điểm của BC, ta có \(\vec{a} = \overrightarrow{BM}\).

3. Tính \(\overrightarrow{GB} + \overrightarrow{GC}\):
- Vì G là trọng tâm của tam giác ABC, ta có các tính chất sau:
- \(\overrightarrow{GB} = \frac{2}{3} \overrightarrow{GM}\)
- \(\overrightarrow{GC} = \frac{2}{3} \overrightarrow{GM}\)

Do đó,
\[
\overrightarrow{GB} + \overrightarrow{GC} = \frac{2}{3} \overrightarrow{GM} + \frac{2}{3} \overrightarrow{GM} = \frac{4}{3} \overrightarrow{GM}
\]

Vì M là trung điểm của BC, ta có \(\overrightarrow{GM} = \frac{1}{2} \overrightarrow{BC}\).

Vậy,
\[
\overrightarrow{GB} + \overrightarrow{GC} = \frac{4}{3} \cdot \frac{1}{2} \overrightarrow{BC} = \frac{2}{3} \overrightarrow{BC}
\]

Như vậy, vectơ \( \overrightarrow{GB} + \overrightarrow{GC} \) là \( \frac{2}{3} \) của vectơ \( \overrightarrow{BC} \).

Cho tam giác đều \(ABC\) có trọng tâm \(G\), điểm \(M\) là trung điểm của cạnh \(BC\). Chúng ta cần xác định các vector \(\vec{a}\), \(\overrightarrow{GB}\) và \(\overrightarrow{GC}\).

**Bước 1: Xác định tọa độ các điểm và vector \(\vec{a}\)**

Giả sử tam giác đều \(ABC\) có cạnh \(BC\) nằm trên trục hoành với trung điểm \(M\) của \(BC\) trùng với gốc tọa độ \(O\). Đặt:

- \(B(-a, 0)\)
- \(C(a, 0)\)

Điểm \(A\) nằm trên đường thẳng vuông góc với \(BC\) và cách đều \(B\), \(C\), nên tọa độ \(A\) là \((0, h)\), với \(h = \sqrt{a^2 - (a/2)^2} = \sqrt{a^2 - a^2/4} = \sqrt{3a^2/4} = \frac{\sqrt{3}}{2}a\).

**Bước 2: Xác định tọa độ trọng tâm \(G\)**

Trọng tâm \(G\) của tam giác đều \(ABC\) có tọa độ được tính bằng trung bình cộng tọa độ các đỉnh:

\[ G \left( \frac{-a + a + 0}{3}, \frac{0 + 0 + \frac{\sqrt{3}}{2}a}{3} \right) = G \left( 0, \frac{\sqrt{3}}{6}a \right) \]

**Bước 3: Xác định vector \(\overrightarrow{GB}\) và \(\overrightarrow{GC}\)**

Vector \(\overrightarrow{GB}\):

\[ \overrightarrow{GB} = B - G = \left( -a - 0, 0 - \frac{\sqrt{3}}{6}a \right) = \left( -a, -\frac{\sqrt{3}}{6}a \right) \]

Vector \(\overrightarrow{GC}\):

\[ \overrightarrow{GC} = C - G = \left( a - 0, 0 - \frac{\sqrt{3}}{6}a \right) = \left( a, -\frac{\sqrt{3}}{6}a \right) \]

**Bước 4: Tính tổng các vector \(\overrightarrow{GB} + \overrightarrow{GC}\)**

\[ \overrightarrow{GB} + \overrightarrow{GC} = \left( -a, -\frac{\sqrt{3}}{6}a \right) + \left( a, -\frac{\sqrt{3}}{6}a \right) = \left( -a + a, -\frac{\sqrt{3}}{6}a - \frac{\sqrt{3}}{6}a \right) = \left( 0, -\frac{\sqrt{3}}{3}a \right) \]

Vậy, tổng các vector \(\overrightarrow{GB} + \overrightarrow{GC}\) là \(\left( 0, -\frac{\sqrt{3}}{3}a \right)\).