Cho tam giác ABC. Trên tia đối của tia AB lấy điểm E sao cho AE=AB,trên tia đối của tia đối của tia AC lấy điểm D sao cho AC=AD . chứng minh rằng:
a)tam giác ABC=tam giác AED b)góc BAM= góc CAM c) AM vuông góc BC
Quảng cáo
2 câu trả lời 674
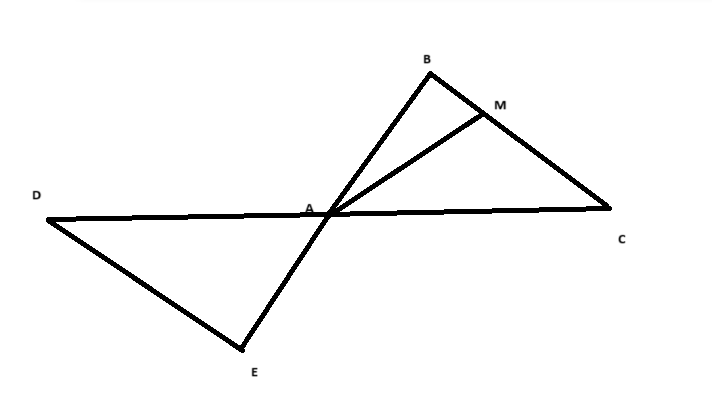
a) Tam giác \( ABC \) đồng dạng với tam giác \( AED \):
- Ta biết \( AE = AB \) và \( AD = AC \). Điều này cho phép chúng ta suy ra \( \triangle AEB \cong \triangle ABC \) và \( \triangle AEC \cong \triangle ACB \) dựa trên trường hợp đồng dạng \( SSS \) (cạnh - cạnh - cạnh).
- Do đó, tam giác \( AED \) cũng đồng dạng với tam giác \( ABC \), vì chúng có các góc tương đương và tỷ lệ các cạnh tương ứng.
b) \( \angle BAM = \angle CAM \):
- Đặt \( M \) là giao điểm của các tia đối của \( AB \) và \( AC \).
- Vì \( AE = AB \) và \( AD = AC \), nên \( E \) và \( D \) là các điểm đối xứng của \( B \) và \( C \) qua \( M \) trên các tia đối của \( AB \) và \( AC \).
- Theo tính chất đối xứng, ta có \( \angle BAM = \angle CAM \).
c) \( AM \) vuông góc \( BC \):
- \( M \) là giao điểm của các tia đối của \( AB \) và \( AC \), được gọi là điểm trung điểm của đoạn thẳng \( BC \).
- Do đó, \( AM \) là đường trung trực của \( BC \), và theo tính chất của đường trung trực trong tam giác, \( AM \) vuông góc \( BC \).
Vậy, từ các lập luận trên, ta đã chứng minh được các phần (a), (b), và (c) của bài toán.
Để chứng minh các điều cần chứng minh, ta sẽ sử dụng các bước sau:
a) Ta có \(AE = AB\) và \(AC = AD\), từ đó ta có thể kết luận rằng tam giác \(AED\) và tam giác \(ABC\) là tam giác cân cân tại \(A\), do đó \(AE = AD\) và góc \(EAD = \frac{1}{2} \angle BAC\). Vì vậy, ta có \(AED = ABC\).
b) Ta có \(AE = AB\) và \(AC = AD\), từ đó ta có thể kết luận rằng tam giác \(AED\) và tam giác \(ABC\) là tam giác cân cân tại \(A\), do đó góc \(EAD = \frac{1}{2} \angle BAC\) và góc \(DAB = \frac{1}{2} \angle BAC\). Vậy góc \(BAM = \angle DAB = \angle CAM\).
c) Ta có \(AE = AB\) và \(AC = AD\), từ đó ta có thể kết luận rằng tam giác \(AED\) và tam giác \(ABC\) là tam giác cân cân tại \(A\), do đó \(AE = AD\). Vậy ta có \(AM\) là đường trung bình của tam giác \(AED\), từ đó ta có \(AM\) vuông góc với \(DE\), hay \(AM\) vuông góc với \(BC\).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


