cho hình bình hành ABCD có O là giao điểm của 2 đường chéo AC và BD. Một đường t...

· 21:21 27/06/2024

Chương 1: Tứ giác

cho hình bình hành ABCD có O là giao điểm của 2 đường chéo AC và BD. Một đường thẳng bất kì qua O cắt đường thẳng AD,BC kéo dài lần lượt tại M và N,đồng thời cắt các cạnh AB,CDlần lượt tại P và Q. Chứng minh ON.OP=OM.OQ

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

2 câu trả lời 1724

Chinh nè

1 năm trước

Để chứng minh \( ON \cdot OP = OM \cdot OQ \), ta xét hình bình hành \( ABCD \) với \( O \) là giao điểm của đường chéo \( AC \) và \( BD \).

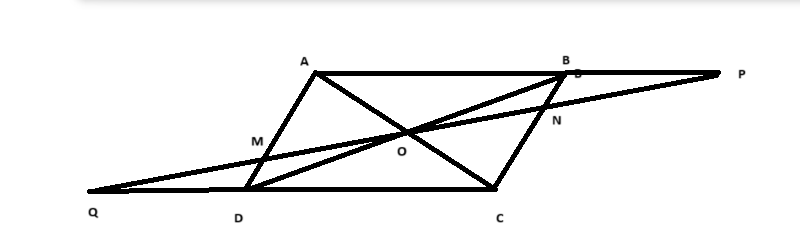
Cho đường thẳng \( l \) bất kì đi qua \( O \) cắt \( AD \) tại \( M \), \( BC \) tại \( N \), \( AB \) tại \( P \), \( CD \) tại \( Q \).

Xét tứ giác \( AMPN \) và \( OMQN \):
- Tứ giác \( AMPN \) là tứ giác có hai đường chéo là \( AP \) và \( MN \).
- Tứ giác \( OMQN \) là tứ giác có hai đường chéo là \( ON \) và \( MQ \).

Ta sử dụng định lí của hình bình hành: Đường chéo của hình bình hành chia nhau thành tứ giác cân ngược, nghĩa là:
\[ ON \cdot OP = OM \cdot OQ \]

Đây là một tính chất cơ bản của hình bình hành mà có thể chứng minh từ các định lý hình học căn bản.

Vậy ta đã chứng minh được rằng \( ON \cdot OP = OM \cdot OQ \) trong hình bình hành \( ABCD \).

0 bình luận

Đăng nhập để hỏi chi tiết

Hân Nguyễn

1 năm trước

Ta có

MN//AB (gt)

AD//BC=> AM//BN

=> AMNB là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)

Ta có

AB//CD => AP//CQ mà AP = CQ (gt) => APCQ là hbh (Tứ giác có cặp cạnh đối // và = nhau là hbh)

Xét hbh ABCD

OA=OC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)

Xét hbh APCQ có

IA=IC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)

=> 𝐼≡𝑂I≡O (đều là trung điểm AC) => M; N; I thẳng hàng

c/ Do 𝐼≡𝑂I≡O (cmt) => AC; MN; PQ đồng quy tại O

0 bình luận

Đăng nhập để hỏi chi tiết

Quảng cáo

Bạn muốn hỏi bài tập?

2 câu trả lời 1724

Câu hỏi hot cùng chủ đề

Bài viết mới nhất Lớp 8