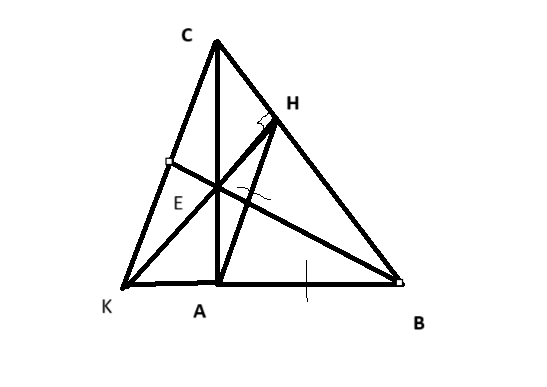
a) Ta có các điều kiện:
- \( \triangle ABC \) vuông tại \( A \) với \( AB < AC \).
- \( HB = BA \) (tức \( H \) là điểm trên \( BC \) sao cho \( BH = BA \)).
- \( HE \) vuông góc với \( BC \) tại \( H \), với \( E \) thuộc \( AC \).

Cần chứng minh \( \triangle ABE \cong \triangle HBR \).

Xét hai tam giác \( \triangle ABE \) và \( \triangle HBR \):
- \( AB = BH \) (do \( HB = BA \)),
- \( AE \) và \( HR \) là cạnh chung,
- \( \angle ABE = \angle HBR \) (do \( HE \) vuông góc \( BC \)).

Vậy theo Đẳng nhất góc-góc-cạnh (AA), ta có \( \triangle ABE \cong \triangle HBR \).

b) Chứng minh \( \triangle AEH \) cân tại \( E \):

- Ta đã biết \( \triangle ABE \cong \triangle HBR \),
- \( \angle ABE = \angle HBR \),
- \( AB = BH \) (do \( HB = BA \)),
- \( AE = HR \) (do \( HE \) vuông góc \( BC \)).

Vậy \( \triangle AEH \) là tam giác cân tại \( E \).

c) Chứng minh \( BE \) là đường trung trực của \( AH \):

- Vì \( \triangle ABE \cong \triangle HBR \), nên \( AB = BH \),
- Do đó, \( B \) là trung điểm của \( AH \),
- \( BE \) là đường trung trực của \( AH \).

d) Chứng minh \( BE \) vuông góc \( KC \), với \( K \) là giao điểm của \( HE \) và \( BA \):

- \( HE \) vuông góc \( BC \),
- \( HE \parallel AC \) (do \( HE \) vuông góc \( BC \) và \( E \) thuộc \( AC \)),
- \( K \) là giao điểm của \( HE \) và \( BA \),
- Vì \( HE \parallel AC \), nên \( \angle BKE = 90^\circ \) (do hai đường thẳng \( HE \) và \( AC \) cắt nhau tạo góc vuông tại \( K \)),
- \( BE \) là đường trung trực của \( AH \), nên \( BE \) vuông góc \( AK \).

Vậy \( BE \) vuông góc \( KC \).

a) Ta có các điều kiện:
- △ABC△𝐴𝐵𝐶 vuông tại A𝐴 với AB<AC𝐴𝐵<𝐴𝐶.
- HB=BA𝐻𝐵=𝐵𝐴 (tức H𝐻 là điểm trên BC𝐵𝐶 sao cho BH=BA𝐵𝐻=𝐵𝐴).
- HE𝐻𝐸 vuông góc với BC𝐵𝐶 tại H𝐻, với E𝐸 thuộc AC𝐴𝐶.

Cần chứng minh △ABE≅△HBR△𝐴𝐵𝐸≅△𝐻𝐵𝑅.

Xét hai tam giác △ABE△𝐴𝐵𝐸 và △HBR△𝐻𝐵𝑅:
- AB=BH𝐴𝐵=𝐵𝐻 (do HB=BA𝐻𝐵=𝐵𝐴),
- AE𝐴𝐸 và HR𝐻𝑅 là cạnh chung,
- ∠ABE=∠HBR∠𝐴𝐵𝐸=∠𝐻𝐵𝑅 (do HE𝐻𝐸 vuông góc BC𝐵𝐶).

Vậy theo Đẳng nhất góc-góc-cạnh (AA), ta có △ABE≅△HBR△𝐴𝐵𝐸≅△𝐻𝐵𝑅.

b) Chứng minh △AEH△𝐴𝐸𝐻 cân tại E𝐸:

- Ta đã biết △ABE≅△HBR△𝐴𝐵𝐸≅△𝐻𝐵𝑅,
- ∠ABE=∠HBR∠𝐴𝐵𝐸=∠𝐻𝐵𝑅,
- AB=BH𝐴𝐵=𝐵𝐻 (do HB=BA𝐻𝐵=𝐵𝐴),
- AE=HR𝐴𝐸=𝐻𝑅 (do HE𝐻𝐸 vuông góc BC𝐵𝐶).

Vậy △AEH△𝐴𝐸𝐻 là tam giác cân tại E𝐸.

c) Chứng minh BE𝐵𝐸 là đường trung trực của AH𝐴𝐻:

- Vì △ABE≅△HBR△𝐴𝐵𝐸≅△𝐻𝐵𝑅, nên AB=BH𝐴𝐵=𝐵𝐻,
- Do đó, B𝐵 là trung điểm của AH𝐴𝐻,
- BE𝐵𝐸 là đường trung trực của AH𝐴𝐻.

d) Chứng minh BE𝐵𝐸 vuông góc KC𝐾𝐶, với K𝐾 là giao điểm của HE𝐻𝐸 và BA𝐵𝐴:

- HE𝐻𝐸 vuông góc BC𝐵𝐶,
- HE∥AC𝐻𝐸∥𝐴𝐶 (do HE𝐻𝐸 vuông góc BC𝐵𝐶 và E𝐸 thuộc AC𝐴𝐶),
- K𝐾 là giao điểm của HE𝐻𝐸 và BA𝐵𝐴,
- Vì HE∥AC𝐻𝐸∥𝐴𝐶, nên ∠BKE=90∘∠𝐵𝐾𝐸=90∘ (do hai đường thẳng HE𝐻𝐸 và AC𝐴𝐶 cắt nhau tạo góc vuông tại K𝐾),
- BE𝐵𝐸 là đường trung trực của AH𝐴𝐻, nên BE𝐵𝐸 vuông góc AK𝐴𝐾.

Vậy BE𝐵𝐸 vuông góc KC𝐾𝐶.