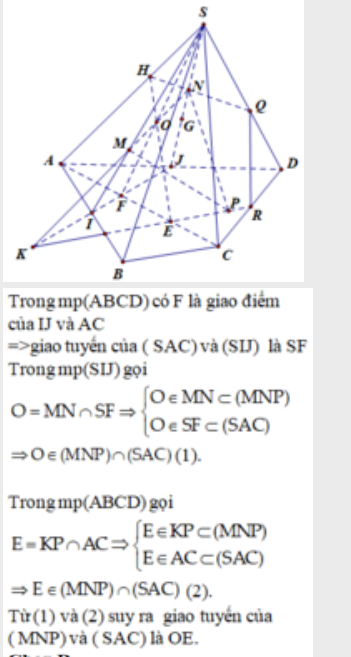
a) $(MNP)$ và $(ABCD)$

 điểm chung thứ nhất:

Vì $P$ nằm trong tứ giác $ABCD$ nên $P \in (ABCD)$. Mặt khác, $P \in (MNP)$ theo giả thiết.

=> $P$ là điểm chung thứ nhất của $(MNP)$ và $(ABCD)$.

 điểm chung thứ hai:

Gọi $I$ là giao điểm của $MN$ và $SD$.

$M$ là trọng tâm tam giác $SAB$ nên $AM$ cắt $SB$ tại trung điểm của $SB$.

$G$ là trọng tâm tam giác $SAD$ nên $AG$ cắt $SD$ tại trung điểm của $SD$.

Do đó, theo định lý Thales đảo trong mặt phẳng $(SBD)$, ta có $MG \parallel BD$.

Suy ra, $MN$ cắt $SD$ tại trung điểm $I$ của $SD$ (vì $MG \parallel BD$ và $N \in SG$).

Gọi $J$ là giao điểm của $PI$ và $AD$.

Ta có:

$I \in SD$, mà $SD \subset (ABCD) \Rightarrow I \in (ABCD)$

$J \in AD$, mà $AD \subset (ABCD) \Rightarrow J \in (ABCD)$

Mặt khác:

$I \in MN$, mà $MN \subset (MNP) \Rightarrow I \in (MNP)$

$J \in PI$, mà $PI \subset (MNP) \Rightarrow J \in (MNP)$

=> $J$ là điểm chung thứ hai của $(MNP)$ và $(ABCD)$.

Vậy giao tuyến của $(MNP)$ và $(ABCD)$ là đường thẳng $PJ$.

b) $(MNP)$ và $(SAC)$

 điểm chung thứ nhất:

Tương tự như trên, ta tìm được điểm chung thứ nhất là $P$.

 điểm chung thứ hai:

Gọi $K$ là giao điểm của $MN$ và $SA$.

Tương tự như trên, ta chứng minh được $MG \parallel BD$.

Áp dụng định lý Thales trong tam giác $SAD$, ta có $\frac{MG}{BD} = \frac{SG}{SD} = \frac{2}{3}$.

Suy ra, $MN$ cắt $SA$ tại điểm $K$ sao cho $SK = \frac{2}{3}SA$.

Ta có:

$K \in SA$, mà $SA \subset (SAC) \Rightarrow K \in (SAC)$

$K \in MN$, mà $MN \subset (MNP) \Rightarrow K \in (MNP)$

=> $K$ là điểm chung thứ hai của $(MNP)$ và $(SAC)$.

Vậy giao tuyến của $(MNP)$ và $(SAC)$ là đường thẳng $PK$.

c) $(MNP)$ và $(SCD)$

 điểm chung thứ nhất:

Ta đã chứng minh được $I$ là trung điểm của $SD$ và $I \in (MNP)$.

=> $I$ là điểm chung thứ nhất của $(MNP)$ và $(SCD)$.

Tìm điểm chung thứ hai:

Gọi $L$ là giao điểm của $PJ$ và $CD$.

Ta có:

$L \in CD$, mà $CD \subset (SCD) \Rightarrow L \in (SCD)$

$L \in PJ$, mà $PJ \subset (MNP) \Rightarrow L \in (MNP)$

=> $L$ là điểm chung thứ hai của $(MNP)$ và $(SCD)$.

Vậy giao tuyến của $(MNP)$ và $(SCD)$ là đường thẳng $IL$.