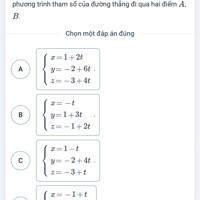
Để tìm phương trình tham số của đường thẳng đi qua hai điểm \( A \) và \( B \) trong không gian \( Oxyz \), chúng ta có thể sử dụng vectơ pháp tuyến của đường thẳng và một điểm trên đường thẳng.

**Bước 1:** Tìm vectơ hướng của đường thẳng bằng vectơ \( \vec{AB} \):
\[ \vec{AB} = B - A \]

**Bước 2:** Chọn một trong hai điểm \( A \) hoặc \( B \) làm điểm trên đường thẳng (ở đây chúng ta chọn \( A \)).

**Bước 3:** Viết phương trình tham số của đường thẳng:

Nếu \( A(x_1, y_1, z_1) \) là một điểm trên đường thẳng và \( \vec{v} = (a, b, c) \) là vectơ hướng của đường thẳng, phương trình tham số của đường thẳng là:
\[ \begin{cases} x = x_1 + at \\ y = y_1 + bt \\ z = z_1 + ct \end{cases} \]

Với \( t \) là tham số.

**Bước 1:** Tính \( \vec{AB} \):
\[ \vec{AB} = B - A = (-1 - 1, 4 - 2, 1 - 3) = (-2, 2, -2) \]

**Bước 2:** Chọn điểm \( A(1, 2, 3) \) làm điểm trên đường thẳng.

**Bước 3:** Viết phương trình tham số của đường thẳng:
\[ \begin{cases} x = 1 - 2t \\ y = 2 + 2t \\ z = 3 - 2t \end{cases} \]

Vậy, phương trình tham số của đường thẳng đi qua hai điểm \( A(1, 2, 3) \) và \( B(-1, 4, 1) \) là:
\[ \begin{cases} x = 1 - 2t \\ y = 2 + 2t \\ z = 3 - 2t \end{cases} \]