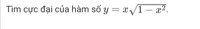Để tìm cực đại của hàm số \( y = x\sqrt{1 - x^2} \), ta thực hiện các bước sau:

### Bước 1: Xác định miền xác định của hàm số

Để hàm số có nghĩa, biểu thức dưới dấu căn phải không âm, tức là \(1 - x^2 \geq 0\). Do đó:

\[ -1 \leq x \leq 1 \]

### Bước 2: Tính đạo hàm của hàm số

Ta dùng quy tắc đạo hàm tích để tính đạo hàm của \( y \):

\[ y = x(1 - x^2)^{1/2} \]

Đạo hàm của \( y \) theo \( x \) là:

\[ y' = \frac{d}{dx} \left( x(1 - x^2)^{1/2} \right) \]

Dùng quy tắc đạo hàm tích:

\[ y' = \frac{d}{dx}(x) \cdot (1 - x^2)^{1/2} + x \cdot \frac{d}{dx}((1 - x^2)^{1/2}) \]

\[ \frac{d}{dx}(x) = 1 \]

\[ \frac{d}{dx}((1 - x^2)^{1/2}) = \frac{1}{2}(1 - x^2)^{-1/2} \cdot (-2x) = -x(1 - x^2)^{-1/2} \]

Do đó:

\[ y' = (1 - x^2)^{1/2} + x \cdot (-x(1 - x^2)^{-1/2}) \]

\[ y' = (1 - x^2)^{1/2} - \frac{x^2}{(1 - x^2)^{1/2}} \]

\[ y' = \frac{(1 - x^2) - x^2}{(1 - x^2)^{1/2}} \]

\[ y' = \frac{1 - 2x^2}{(1 - x^2)^{1/2}} \]

### Bước 3: Tìm các điểm tới hạn

Ta giải phương trình \( y' = 0 \):

\[ \frac{1 - 2x^2}{(1 - x^2)^{1/2}} = 0 \]

Điều này xảy ra khi tử số bằng 0:

\[ 1 - 2x^2 = 0 \]

\[ 2x^2 = 1 \]

\[ x^2 = \frac{1}{2} \]

\[ x = \pm \frac{1}{\sqrt{2}} = \pm \frac{\sqrt{2}}{2} \]

### Bước 4: Xét dấu của đạo hàm trên các khoảng để tìm cực trị

Ta xét dấu của \( y' \) trên các khoảng \([-1, -\frac{\sqrt{2}}{2})\), \([- \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}]\) và \([\frac{\sqrt{2}}{2}, 1]\):

- Khi \( x \in \left( -1, -\frac{\sqrt{2}}{2} \right) \) hoặc \( x \in \left( \frac{\sqrt{2}}{2}, 1 \right) \), ta có \( 1 - 2x^2 < 0 \), nên \( y' < 0 \).

- Khi \( x \in \left( -\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) \), ta có \( 1 - 2x^2 > 0 \), nên \( y' > 0 \).

### Bước 5: Tính giá trị hàm số tại các điểm tới hạn và các điểm biên

Ta tính giá trị của hàm số tại các điểm \( x = \pm \frac{\sqrt{2}}{2} \), \( x = -1 \), và \( x = 1 \).

- Tại \( x = \frac{\sqrt{2}}{2} \):

\[ y = \frac{\sqrt{2}}{2} \sqrt{1 - \left( \frac{\sqrt{2}}{2} \right)^2} = \frac{\sqrt{2}}{2} \sqrt{1 - \frac{1}{2}} = \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{2}}{2} = \frac{2}{4} = \frac{1}{2} \]

- Tại \( x = -\frac{\sqrt{2}}{2} \):

\[ y = -\frac{\sqrt{2}}{2} \sqrt{1 - \left( -\frac{\sqrt{2}}{2} \right)^2} = -\frac{\sqrt{2}}{2} \sqrt{1 - \frac{1}{2}} = -\frac{\sqrt{2}}{2} \cdot \frac{\sqrt{2}}{2} = -\frac{2}{4} = -\frac{1}{2} \]

- Tại \( x = 1 \) và \( x = -1 \):

\[ y = x\sqrt{1 - x^2} = 1 \cdot \sqrt{1 - 1} = 1 \cdot 0 = 0 \]

Từ các kết quả trên, ta thấy rằng giá trị cực đại của hàm số \( y = x\sqrt{1 - x^2} \) là \( \frac{1}{2} \), xảy ra tại \( x = \frac{\sqrt{2}}{2} \).

Vậy, cực đại của hàm số \( y = x\sqrt{1 - x^2} \) là:

\[ \frac{1}{2} \]