Cho tứ giác ABCD, gọi P, Q là trung điểm của đường chéo AC và BD. Chứng minh rằn

Nhân_Thành11

Đã trả lời bởi chuyên gia

· 09:10 05/06/2024

Đã trả lời bởi chuyên gia

Cho tứ giác ABCD, gọi P, Q là trung điểm của đường chéo AC và BD. Chứng minh rằng $|\frac{A B - C D}{2}| \leq P Q < \frac{A B + C D}{2}$

Trả Lời (+5 điểm)

Lưu câu hỏi Lưu

Hỏi chi tiết

Quảng cáo

2 câu trả lời 397

Phạm Thị Huyền

1 năm trước

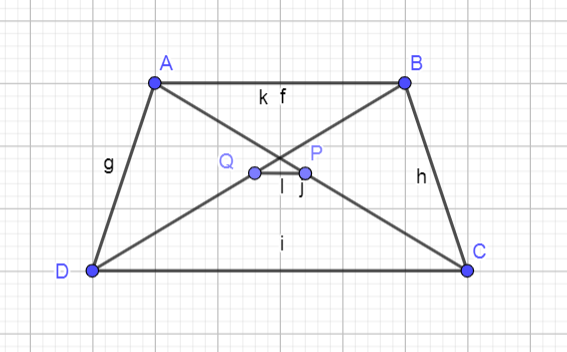
Để chứng minh bất đẳng thức $ \left| \frac{AB - CD}{2} \right| \leq PQ < \frac{AB + CD}{2} $ với $ P $ và $ Q $ là trung điểm của các đường chéo $ AC $ và $ BD $ của tứ giác $ ABCD $, ta thực hiện các bước như sau:

### 1. Tính khoảng cách $ PQ $
Gọi $ P $ và $ Q $ lần lượt là trung điểm của $ AC $ và $ BD $.
Theo định nghĩa, tọa độ của $ P $ và $ Q $ lần lượt là:
\[ P = \left( \frac{A + C}{2} \right), \quad Q = \left( \frac{B + D}{2} \right) \]

Ta cần tính độ dài $ PQ $:
\[ PQ = \left| P - Q \right| = \left| \frac{A + C}{2} - \frac{B + D}{2} \right| = \frac{1}{2} \left| (A + C) - (B + D) \right| \]

### 2. Sử dụng bất đẳng thức tam giác
Sử dụng bất đẳng thức tam giác cho độ dài của các đoạn thẳng trên mặt phẳng:
\[ \left| (A + C) - (B + D) \right| \geq \left| |A - B| - |C - D| \right| \]
\[ \left| (A + C) - (B + D) \right| \leq |A - B| + |C - D| \]

Do đó, ta có:
\[ \frac{1}{2} \left| (A + C) - (B + D) \right| \geq \frac{1}{2} \left| |A - B| - |C - D| \right| \]
\[ \frac{1}{2} \left| (A + C) - (B + D) \right| \leq \frac{1}{2} (|A - B| + |C - D|) \]

### 3. Áp dụng vào khoảng cách $ PQ $
Vậy ta suy ra:
\[ PQ \geq \frac{1}{2} \left| |A - B| - |C - D| \right| \]
\[ PQ \leq \frac{1}{2} (|A - B| + |C - D|) \]

### 4. Đặt $ AB = |A - B| $ và $ CD = |C - D| $
Ta có:
\[ \frac{1}{2} \left| AB - CD \right| \leq PQ \]
\[ PQ \leq \frac{1}{2} (AB + CD) \]

### Kết luận:
Do đó, bất đẳng thức cần chứng minh là:
\[ \left| \frac{AB - CD}{2} \right| \leq PQ < \frac{AB + CD}{2} \]

Đã được chứng minh dựa trên việc sử dụng định nghĩa trung điểm và bất đẳng thức tam giác cho khoảng cách giữa hai điểm trong mặt phẳng.

...Xem thêm

0 bình luận

1 ( 1.0 )

Đăng nhập để hỏi chi tiết