Quảng cáo
2 câu trả lời 531
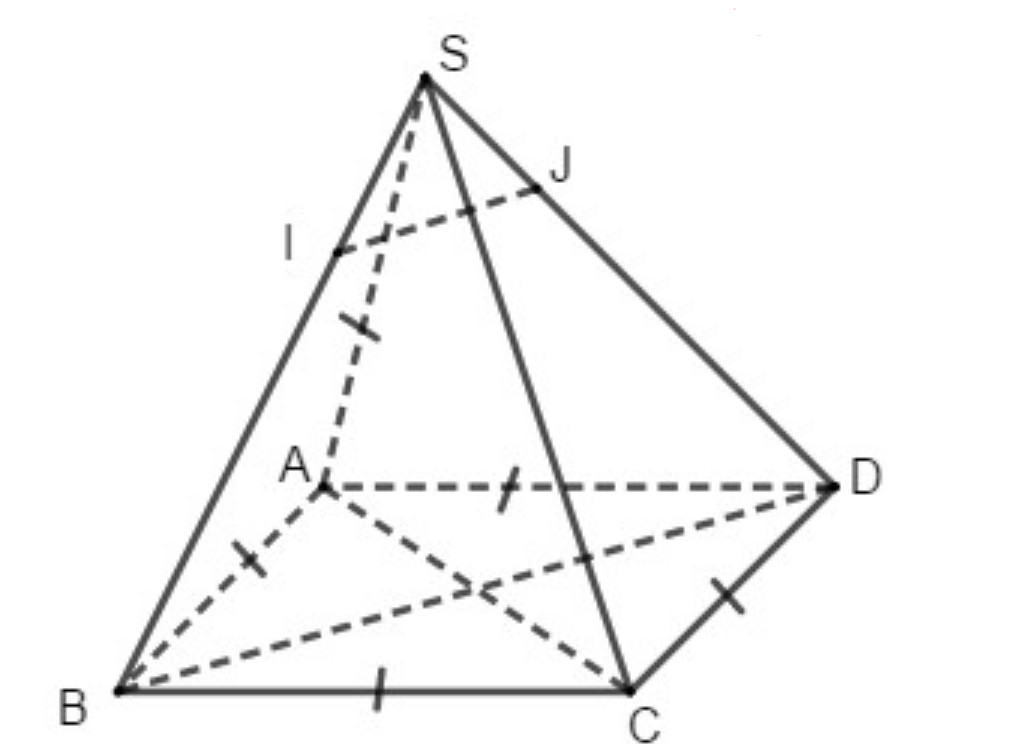 Ta có BC//AD
Ta có BC//AD
SA vuông góc BC
=>SA vuông góc AD =>∠SAD= 90độ
=> (SD,BC)=(SD,AD)= ∠SDA
SA=AB
AB=AD (ABCD là hình thoi)
=>SA=AD
Xét tam giác vuông SAD vuông tại A, ta có
tan SDA=SAAD =1 =>∠SDA=45 độ
(SD,BC)=(SD,AD)= ∠SDA=45 độ
Xét tam giác ABC: $AB=BC$ và $\angle ABC = 60^\circ$ (vì ABCD là hình thoi).
Suy ra tam giác ABC đều.
Do đó, $AC = AB\sqrt{3} = SA\sqrt{3}$.
Xét tam giác SAC vuông tại A:
$SC^2 = SA^2 + AC^2 = SA^2 + 3SA^2 = 4SA^2$.
Suy ra $SC = 2SA$.
Xét tam giác SDB:
$SB = SC = 2SA$.
$SD = \sqrt{SA^2 + AD^2} = \sqrt{SA^2 + 2SA^2} = SA\sqrt{3}$.
Áp dụng định lí cosin trong tam giác SDB:
$BD^2 = SB^2 + SD^2 - 2SB.SD.\cos \angle SDB$.
$4SA^2 = 4SA^2 + 3SA^2 - 2.2SA.SA\sqrt{3}.\cos \angle SDB$.
$\cos \angle SDB = \frac{1}{2\sqrt{3}}$.
Suy ra $\angle SDB = \arccos \frac{1}{2\sqrt{3}}$.
Xét tam giác SDM:
$\angle SDM = 180^\circ - \angle SDB = 180^\circ - \arccos \frac{1}{2\sqrt{3}}$.
Kết luận:
Góc giữa hai đường thẳng SD và BC là $\boxed{180^\circ - \arccos \frac{1}{2\sqrt{3}}}$.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
134838
Đã trả lời bởi chuyên gia
134838 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
75920
Đã trả lời bởi chuyên gia
75920 -
 Đã trả lời bởi chuyên gia
71641
Đã trả lời bởi chuyên gia
71641 -
 Đã trả lời bởi chuyên gia
47575
Đã trả lời bởi chuyên gia
47575


