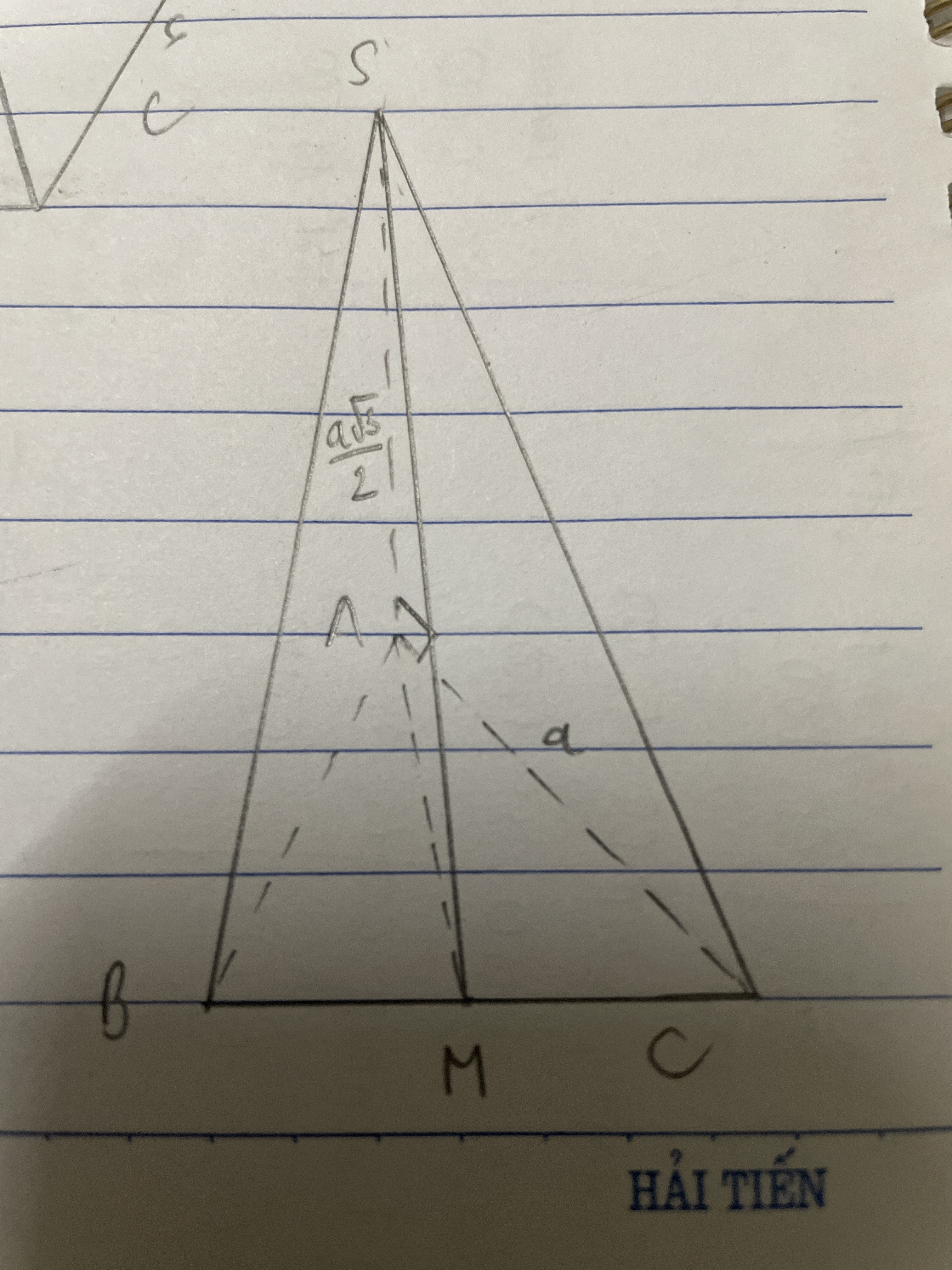
Để tìm góc giữa đường thẳng \( SM \) và mặt phẳng đáy \( ABC \) trong hình chóp \( S.ABC \), ta làm như sau:

1. **Định vị các điểm và các vectơ:**
- \( A, B, C \) là các đỉnh của tam giác đều cạnh \( a \).
- \( S \) là đỉnh chóp sao cho \( SA \) vuông góc với mặt phẳng đáy \( ABC \) và \( SA = \frac{a \sqrt{3}}{2} \).
- \( M \) là trung điểm của \( BC \), do đó \( M \) có tọa độ trung bình của \( B \) và \( C \).

2. **Hệ tọa độ:**
Chúng ta đặt hệ tọa độ sao cho:
- \( A \) tại \( (0, 0, 0) \).
- \( B \) tại \( \left( a, 0, 0 \right) \).
- \( C \) tại \( \left( \frac{a}{2}, \frac{a\sqrt{3}}{2}, 0 \right) \).

3. **Tọa độ của điểm \( M \):**
\[
M = \left( \frac{a + \frac{a}{2}}{2}, \frac{0 + \frac{a\sqrt{3}}{2}}{2}, 0 \right) = \left( \frac{3a}{4}, \frac{a\sqrt{3}}{4}, 0 \right)
\]

4. **Tọa độ của điểm \( S \):**
\[
S = \left( 0, 0, \frac{a\sqrt{3}}{2} \right)
\]

5. **Vectơ \( \overrightarrow{SM} \):**
\[
\overrightarrow{SM} = M - S = \left( \frac{3a}{4}, \frac{a\sqrt{3}}{4}, 0 \right) - \left( 0, 0, \frac{a\sqrt{3}}{2} \right) = \left( \frac{3a}{4}, \frac{a\sqrt{3}}{4}, -\frac{a\sqrt{3}}{2} \right)
\]

6. **Góc giữa \( \overrightarrow{SM} \) và mặt phẳng đáy \( ABC \):**
- Để tìm góc giữa \( \overrightarrow{SM} \) và mặt phẳng \( ABC \), ta cần tính góc giữa \( \overrightarrow{SM} \) và đường thẳng vuông góc với mặt phẳng \( ABC \), đó là \( SA \).

Vectơ \( \overrightarrow{SA} \) có tọa độ:
\[
\overrightarrow{SA} = A - S = \left( 0, 0, 0 \right) - \left( 0, 0, \frac{a\sqrt{3}}{2} \right) = \left( 0, 0, -\frac{a\sqrt{3}}{2} \right)
\]

- Ta dùng công thức cosin giữa hai vectơ:
\[
\cos \theta = \frac{\overrightarrow{SM} \cdot \overrightarrow{SA}}{\|\overrightarrow{SM}\| \|\overrightarrow{SA}\|}
\]

- Tích vô hướng \( \overrightarrow{SM} \cdot \overrightarrow{SA} \):
\[
\overrightarrow{SM} \cdot \overrightarrow{SA} = \left( \frac{3a}{4}, \frac{a\sqrt{3}}{4}, -\frac{a\sqrt{3}}{2} \right) \cdot \left( 0, 0, -\frac{a\sqrt{3}}{2} \right) = \left( 0 + 0 + \left( -\frac{a\sqrt{3}}{2} \right) \left( -\frac{a\sqrt{3}}{2} \right) \right) = \frac{3a^2}{4}
\]

- Độ dài của \( \overrightarrow{SM} \):
\[
\|\overrightarrow{SM}\| = \sqrt{\left( \frac{3a}{4} \right)^2 + \left( \frac{a\sqrt{3}}{4} \right)^2 + \left( -\frac{a\sqrt{3}}{2} \right)^2 } = \sqrt{\frac{9a^2}{16} + \frac{3a^2}{16} + \frac{3a^2}{4}} = \sqrt{\frac{15a^2}{16}} = \frac{\sqrt{15}a}{4}
\]

- Độ dài của \( \overrightarrow{SA} \):
\[
\|\overrightarrow{SA}\| = \left| -\frac{a\sqrt{3}}{2} \right| = \frac{a\sqrt{3}}{2}
\]

- Tính \( \cos \theta \):
\[
\cos \theta = \frac{\frac{3a^2}{4}}{\frac{\sqrt{15}a}{4} \cdot \frac{a\sqrt{3}}{2}} = \frac{\frac{3a^2}{4}}{\frac{a^2 \sqrt{45}}{8}} = \frac{3a^2}{\frac{a^2 3\sqrt{5}}{4}} = \frac{12}{3\sqrt{5}} = \frac{4}{\sqrt{5}} = \frac{4\sqrt{5}}{5}
\]

- Góc giữa \( \overrightarrow{SM} \) và \( \overrightarrow{SA} \) là \( \theta = \arccos \left( \frac{4\sqrt{5}}{5} \right) \).

- Vì \( SA \) vuông góc với mặt phẳng đáy nên góc giữa \( SM \) và mặt phẳng đáy là góc bù của \( \theta \).

- Sử dụng kết quả tính toán:

\[
\cos \left( 90^\circ - \theta \right) = \sin \theta = \sqrt{1 - \cos^2 \theta} = \sqrt{1 - \left( \frac{4\sqrt{5}}{5} \right)^2} = \sqrt{\frac{1}{5}} = \frac{1}{\sqrt{5}} = \frac{\sqrt{5}}{5}
\]

Vậy, đáp án chính xác là \( \theta = 30^\circ \).

Do đó, góc giữa đường thẳng \( SM \) và mặt phẳng đáy bằng \( \boxed{30^\circ} \).