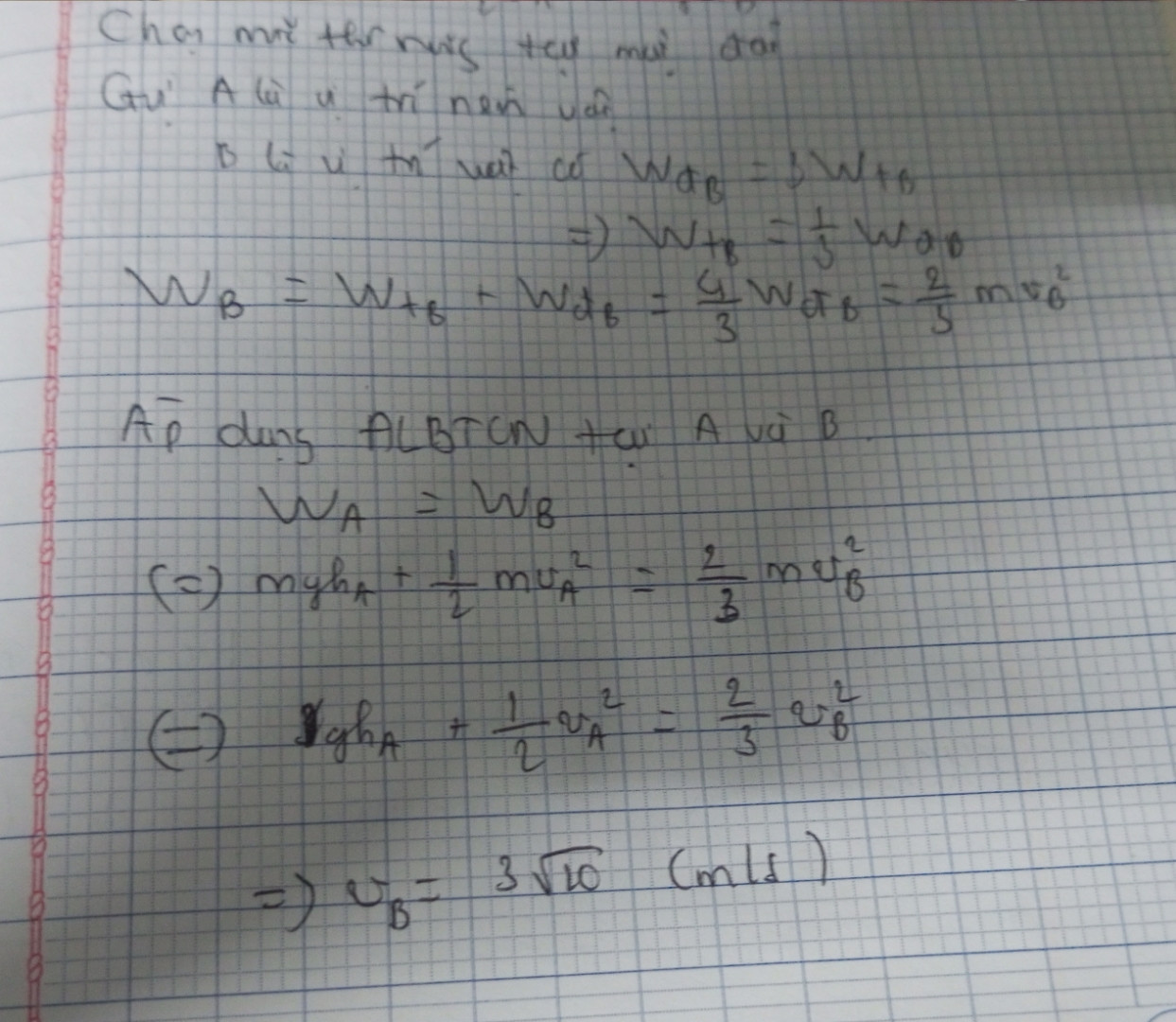
Khi một vật được ném thẳng đứng lên trên từ độ cao 1m với vận tốc ban đầu 10 m/s, ta tìm được động năng và cơ năng tại điểm có vận tốc bn.

Đầu tiên chúng ta hãy tìm thời gian để vật đạt tới điểm có vận tốc bằng bn. Chúng ta có thể sử dụng phương trình sau để tìm thời gian:

v = u + tại

trong đó: v = vận tốc cuối cùng (bn) u = vận tốc ban đầu (10 m/s) a = gia tốc trọng trường (-10 m/s^2) t = thời gian

Vì vậy chúng tôi có:

bn = 10 - 10t

Vì thế,

t = (10 - bn) / 10

Bây giờ, chúng ta có thể tìm động năng tại điểm này bằng phương trình sau:

Năng lượng động = (1/2) * m * (bn)^2

trong đó: m = khối lượng của vật

Cơ năng tại điểm ban đầu bằng tổng thế năng và động năng:

Cơ năng = Thế năng + Động năng

Thế năng = m * g * h = m * 10 * 1 = 10m (vì h = 1m)

Động năng = (1/2) * m * (10)^2 = 50m

Vì thế,

Cơ năng = 10m + 50m = 60m

Theo bài toán, động năng bằng ba lần cơ năng khi vận tốc là bn. Vì vậy, chúng ta có thể viết phương trình sau:

(1/2) * m * (bn)^2 = 3 * 60m

Đơn giản hóa, chúng tôi nhận được:

(1/2) * (bn)^2 = 180m

Vì thế,

(bn)^2 = 360m

bn = sqrt(360m)

Vậy vận tốc của vật tại điểm có động năng gấp 3 lần cơ năng là bn= sqrt(360m).