Quảng cáo
2 câu trả lời 322
Để tìm tọa độ đỉnh của parabol \( y = x^2 - 20x + 10 \), chúng ta có thể sử dụng công thức hoàn thiện bậc hai hoặc hoàn thành bình phương.
Công thức hoàn thiện bậc hai cho một hàm số bậc hai \( ax^2 + bx + c \) là:
\[ x_{\text{đỉnh}} = -\frac{b}{2a} \]
Ở đây, \( a = 1 \) (hệ số của \( x^2 \)) và \( b = -20 \) (hệ số của \( x \)).
Thay vào công thức, ta có:
\[ x_{\text{đỉnh}} = -\frac{-20}{2 \cdot 1} = \frac{20}{2} = 10 \]
Sau đó, để tìm \( y \) tương ứng với \( x_{\text{đỉnh}} \), ta thay \( x = 10 \) vào phương trình \( y = x^2 - 20x + 10 \):
\[ y = (10)^2 - 20(10) + 10 = 100 - 200 + 10 = -90 \]
Vậy, tọa độ đỉnh của parabol là \( (10, -90) \).
(P) : y = ax2 + bx + c
Parabol có đỉnh I(1 ; 4) ⇒ –b/2a = 1 ⇒ b = –2a ⇒ 2a + b = 0.
Parabol đi qua I(1; 4) ⇒ 4 = a.12 + b . 1 + c ⇒ a + b + c = 4.
Paraol đi qua D(3; 0) ⇒ 0 = a.32 + b.3 + c ⇒ 9a + 3b + c = 0.
Giải hệ phương trình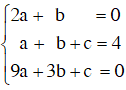 
ta được : a = –1 ; b = 2 ; c = 3.
Vậy a = –1 ; b = 2 ; c = 3.
Quảng cáo
Bạn hỏi - Chuyên gia trả lời
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Đã trả lời bởi chuyên gia
89101 -
Đã trả lời bởi chuyên gia
59778
-
Hỏi từ APP VIETJACK
Đã trả lời bởi chuyên gia
58982
-
Đã trả lời bởi chuyên gia
50860
-
Hỏi từ APP VIETJACK
Đã trả lời bởi chuyên gia
48304
-
Đã trả lời bởi chuyên gia
38597
-
보고 싶어요
2885 điểm
-
meluynsu 🤗
1435 điểm
-
🐟祖尼⚡
1300 điểm
-
❤︎루미❤︎
1100 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
1035 điểm
-
`color{blue}text{HuyTùng☢`
1015 điểm
-
Ben 10K
645 điểm
-
≽^•⩊•^≼ 🐾😻
590 điểm
-
⋅˚₊‧ ଳ⋆.࿔*:･Ⓗồⓝⓖ´꒳`
575 điểm
-
𝘳𝘺𝘯.𝘭𝘦𝘦ッ
550 điểm
-
Kiều Anh 525 điểm
-
devestro
520 điểm
-
Lộc Hữu 515 điểm
-
`有缘再相见 `
480 điểm
-
jgdmaX
345 điểm
Rút gọn
