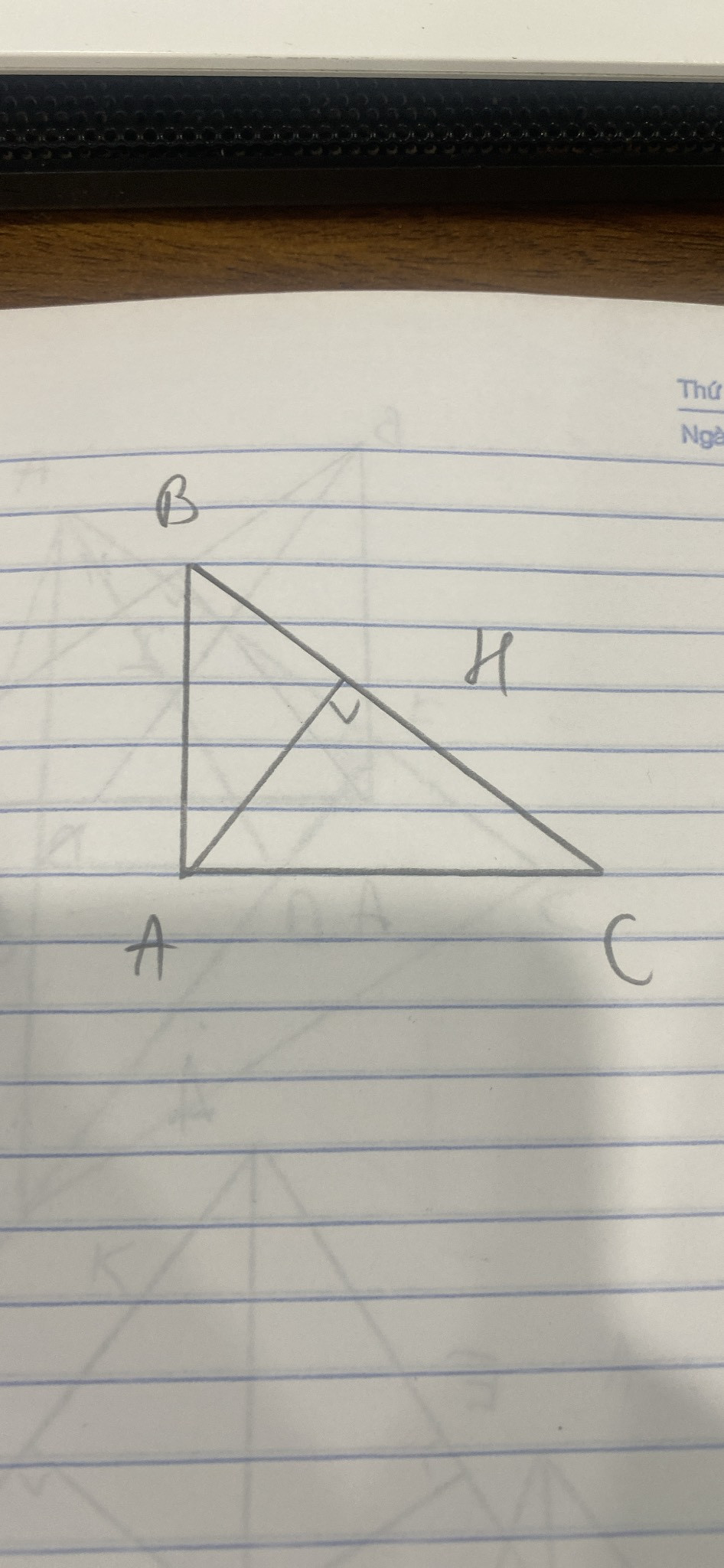
Để giải bài toán này, chúng ta sẽ thực hiện các bước sau:

### a) Tính \( BC \), \( AH \), \( BH \), \( CH \) và chứng minh \( \triangle ABC \) đồng dạng với \( \triangle HBA \):

Với tam giác vuông \( \triangle ABC \), ta có:

1. \( AB = 6 \) và \( AC = 8 \).
2. Sử dụng định lý Pythagoras, ta tính được \( BC \):
\[ BC = \sqrt{AB^2 + AC^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \].
3. Diện tích của \( \triangle ABC \) có thể tính được bằng \( \frac{1}{2} \times AB \times AC = \frac{1}{2} \times 6 \times 8 = 24 \).
4. Do diện tích của một tam giác bằng nửa tích của độ dài hai cạnh nhân với độ dài đường cao tương ứng, ta có:
\[ \frac{1}{2} \times AB \times AC = \frac{1}{2} \times AH \times BC \Rightarrow AH = \frac{AB \times AC}{BC} = \frac{6 \times 8}{10} = \frac{48}{10} = 4.8 \].
5. Ta biết \( AH = 4.8 \), từ đó, đường cao \( AH \) chia \( BC \) thành đoạn \( BH \) và \( HC \) sao cho \( BH = \frac{AB^2}{BC} \) và \( HC = \frac{AC^2}{BC} \).
\[ BH = \frac{AB^2}{BC} = \frac{6^2}{10} = \frac{36}{10} = 3.6 \].
\[ HC = \frac{AC^2}{BC} = \frac{8^2}{10} = \frac{64}{10} = 6.4 \].

Suy ra \( BH = 3.6 \) và \( HC = 6.4 \).

Ta đã có các giá trị cần thiết cho phần sau.

### Chứng minh \( \triangle ABC \) đồng dạng với \( \triangle HBA \):

Ta thấy rằng \( \triangle ABC \) và \( \triangle HBA \) đều có một góc vuông ở \( A \). Cũng như:
- \( \angle ABC = \angle HBA \) (cùng là góc vuông).
- \( \angle BAC = \angle ABH \) (vì chúng bù cho nhau).

Vậy, theo góc-góc giống nhau, ta kết luận được \( \triangle ABC \) đồng dạng với \( \triangle HBA \).

### b) Tính \( AH \), \( DH \), \( HC \), \( CY \):

Với \( \triangle ABC \), ta đã tính được \( AH = 4.8 \).

Xét \( \triangle ABC \), ta cũng biết \( \angle ABC = 90^\circ \). Do đó, đường phân giác của góc \( \angle ABC \) cắt \( AC \) tại \( Y \) sao cho:
\[ \frac{AY}{CY} = \frac{AB}{BC} = \frac{6}{10} = 0.6 \].

Vậy, \( AY = 0.6 \times AC = 0.6 \times 8 = 4.8 \).

Như vậy, \( YC = AC - AY = 8 - 4.8 = 3.2 \).

Với tam giác vuông \( \triangle AYC \), ta có thể tính được \( CY \) bằng cách sử dụng định lý Pythagoras:
\[ CY = \sqrt{AC^2 - AY^2} = \sqrt{8^2 - 4.8^2} \approx \sqrt{64 - 23.04} \approx \sqrt{40.96} \approx 6.4 \].

Vậy, \( CY \approx 6.4 \).

### Kết luận:

a) Ta đã chứng minh được \( \triangle ABC \) đồng dạng với \( \triangle HBA \).

b) \( AH = 4.8 \), \( CY \approx 6.4 \).