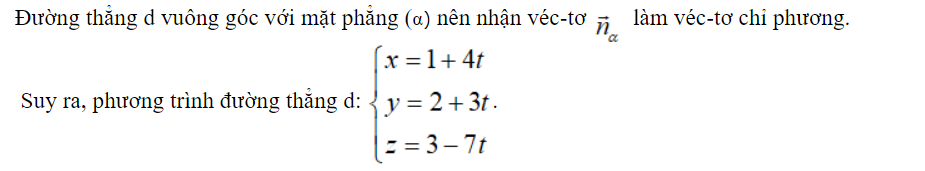Quảng cáo
5 câu trả lời 223
Đường thẳng \( d \) đi qua điểm \( A(1; 2; 3) \) và vuông góc với mặt phẳng \( (α): 4x + 3y - 7z + 1 = 0 \) sẽ có một vectơ chỉ phương là vectơ pháp tuyến của mặt phẳng \( (α) \), tức là \( \vec{n} = (4; 3; -7) \).
Vậy, phương trình tham số của đường thẳng \( d \) là:
$\begin{cases}x = 1 + 4t \\y = 2 + 3t \\z = 3 - 7t\end{cases}$
trong đó \( t \) là tham số.
Đường thẳng d� đi qua điểm A(1;2;3)�(1;2;3) và vuông góc với mặt phẳng (α):4x+3y−7z+1=0(α):4�+3�−7�+1=0 sẽ có một vectơ chỉ phương là vectơ pháp tuyến của mặt phẳng (α)(α), tức là →n=(4;3;−7)�→=(4;3;−7).
Vậy, phương trình tham số của đường thẳng d� là:
⎧⎨⎩x=1+4ty=2+3tz=3−7t
Quảng cáo
Bạn muốn hỏi bài tập?