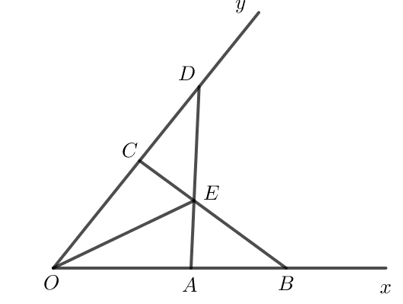
A) AD = BC
B) tam giác eab = tam giác ecd
D) là tia phân giác của góc xOy
Quảng cáo
2 câu trả lời 574
Để chứng minh các phần trong bài toán, ta thực hiện các bước sau:
A) Chứng minh AD = BC:
1. Vẽ đoạn thẳng OA và OB.
2. Theo giả thiết, OA < OB.
3. Kẻ đoạn thẳng OD sao cho OD = OB và OD nằm trên tia OY.
4. Vì OA = OX, OD = OB, nên tam giác OAD và OBC là tam giác cân tại O.
5. Do đó, ta có AD = 2 * OA và BC = 2 * OB.
6. Vì OA < OB nên AD = BC.
B) Chứng minh tam giác EAB = tam giác ECD:
1. Vẽ đoạn thẳng AE và CD.
2. Ta có OA = OX, OD = OB (theo giả thiết).
3. Do đó, tam giác OAX và ODO là tam giác đều.
4. Kẻ OE và OC là tia phân giác của các góc AOX và DOB.
5. Ta có OA = OX, OD = OB, và OE = OC (theo bài toán).
6. Do đó, tam giác OAE = tam giác ODC (tam giác đều).
7. Từ đó suy ra tam giác EAB = tam giác ECD (do tương đương với tam giác OAE = tam giác ODC).
C) Chứng minh DE là tia phân giác của góc xOy:
1. Do AE = CD và AB = EC (vì tam giác EAB = tam giác ECD).
2. Vì tam giác ABE = tam giác DCE, nên các góc tương ứng bằng nhau.
3. Vậy DE là tia phân giác của góc xOy.
Như vậy, ta đã chứng minh đúng các phần trong bài toán.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757