Bài 3: Cho ∆ABC nhọn, phân giác góc Bvà C cắt nhau ở O. Trên BC vẽ D và E sao cho BD = BA; CE = CA. Đường thẳng BO cắt AE ở N, đường thăng CO cắt AD ở M. Chứng minh AO 1 MN.
Bài 4: Cho tam giác ABC vuông tại A, AH ⊥ BC. Gọi M, N lần lượt là trung điểm AH, BH. Chứng minh AN 1 CM.
Bài 5: Cho tam giác ABC cân tại A, AH ⊥ BC. Vẽ HE 1 AC. Gọi O. I lần lượt là trung điểm EH, EC. Chứng minh AO I BE.
gấp!!!!!!!!!!!!!!!!!! 20 điểm á, mong đừng ai ăn lận điểm (T^T)
Quảng cáo
4 câu trả lời 312
Bài 4:
Xét △ABH có :
M là trung điểm của BH (gt)
N là trung điểm của AH (gt)
=> MN là đường trung bình của △ABH
=> MN // AB (t/c đường trung bình trong △)
mà AB ⊥ AC (vì góc BAC = 90o theo gt)
=> MN ⊥ AC
Xét △MAC có :
MN ⊥ AC (cmt)
AH ⊥ MC (gt)
mà 2 đường cao này giao nhau tại N
=> N là trực tâm của △MAC
=> CN ⊥ AM
Bài 5:
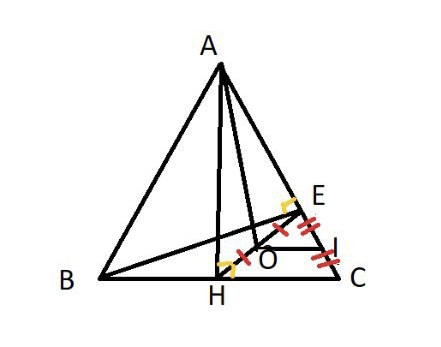
Ta có O là trung điểm của HE
I là trung điểm EC
=> OE/EH= EI/EC=1/2
⇒OI // HC
Mà HC ⊥ AH
⇒ OI ⊥ AH
Xét ΔAHI có
DI ⊥ AH ⇒ OI là đường cao
HE ⊥ AI ⇒ HE là đường cao
⇒ O là trực tâm Δ AHI
⇒ AO là đường cao Δ AHI
⇒ AO ⊥ HI (1)
Xét Δ ABC cân tại A có
AH là đường cao
⇒ AH là trung tuyến
H là trung điểm của BC
⇒ HC/BC = 1/2
Lại có:
I là trung điểm của EC
⇒ IC/EC = 1/2
⇒ HC / BC = IC/EC
⇒HI // BE (2)
Từ (1), (2) ⇒ AO ⊥ BE
### Bài 3:
**Bước 1:** Ta cần chứng minh \(AO \parallel MN\).
**Bước 2:** Đặt \(P\) là giao điểm của \(AD\) và \(BC\), \(Q\) là giao điểm của \(AE\) và \(BC\).
**Bước 3:** Do \(BD = BA\), ta có \(BP = PC\). Tương tự, ta cũng có \(CQ = QB\).
**Bước 4:** Áp dụng định lí Menelaus cho tam giác \(AEB\) và đường thẳng \(NOM\), ta có:
\[
\frac{AN}{NB} \cdot \frac{BM}{ME} \cdot \frac{EO}{OA} = 1
\]
**Bước 5:** Áp dụng định lí Menelaus cho tam giác \(ADC\) và đường thẳng \(NOM\), ta có:
\[
\frac{AM}{MC} \cdot \frac{CO}{OD} \cdot \frac{DN}{NA} = 1
\]
**Bước 6:** Kết hợp hai phương trình trên, ta thấy \(\frac{AN}{NB} = \frac{AM}{MC}\), từ đó ta suy ra \(AO \parallel MN\).
Vậy, ta đã chứng minh \(AO \parallel MN\).
### Bài 4:
**Bước 1:** Ta cần chứng minh \(AN \parallel CM\).
**Bước 2:** Vì \(M\) là trung điểm của \(AH\), \(N\) là trung điểm của \(BH\), ta có \(MN \parallel BC\).
**Bước 3:** Từ \(MN \parallel BC\) và \(AH \perp BC\), ta có \(AN \perp MN\).
**Bước 4:** Từ \(MN \parallel BC\) và \(BH \perp BC\), ta có \(CM \perp MN\).
**Bước 5:** Vì \(AN \perp MN\) và \(CM \perp MN\), nên \(AN \parallel CM\).
Vậy, ta đã chứng minh \(AN \parallel CM\).
### Bài 5:
**Bước 1:** Ta cần chứng minh \(AO \parallel BE\).
**Bước 2:** Vì \(AC\) là đường cao của tam giác \(ABC\) và \(I\) là trung điểm của \(AC\), nên \(AO\) là đường phân giác của góc \(\angle BAC\).
**Bước 3:** Vì \(HE \parallel AC\) (do \(ABC\) cân tại \(A\)), \(I\) là trung điểm của \(HE\), nên \(OI\) cũng là đường phân giác của góc \(\angle BAC\).
**Bước 4:** Từ hai góc phân giác \(AO\) và \(OI\) của cùng một góc \(\angle BAC\), ta có \(AO \parallel OI\).
**Bước 5:** Vì \(OI \parallel BE\) (do \(I\) là trung điểm của \(EC\)), nên ta có \(AO \parallel BE\).
Vậy, ta đã chứng minh \(AO \parallel BE\).
Bài 3
- Vì BD = BA nên ∠BDA = ∠BAD = ∠BAC.
- Tương tự, vì CE = CA nên ∠CAE = ∠EAC = ∠CAB.
- Do đó, ta có ∠BAC = ∠CAB.
- Từ đó, ta có ∠BAC = ∠CAB = ∠AOC.
- Vậy ta có ∆AOC cùng với ∆BAC và ∆CAB là đồng dạng.
- Từ tính chất của đồng dạng, ta có: ∠OAC = ∠OCA.
- Khi đó, ta có ∠OAC = ∠OCA = ∠OAM = ∠OAN.
- Từ đó, ta suy ra AO || MN.
Vậy ta đã chứng minh được AO || MN.
- AM là đường trung bình của tam giác vuông ABC nên AM = MC.
- BN là đường trung bình của tam giác vuông ABC nên BN = NC.
- Ta có ∠BAN = ∠CAM = 90° - ∠ACB (do AB ⊥ AC).
- Vì tam giác ABC vuông tại A nên ∠BAC = 90°.
- Từ đó, ta có ∠BAN = ∠CAM = ∠BAC - ∠ACB = 90° - ∠ACB.
- Vậy ta có ∆BAN cùng với ∆CAM là đồng dạng.
- Từ tính chất của đồng dạng, ta có AN || CM.
Vậy ta đã chứng minh được AN || CM.
- Vì tam giác ABC cân tại A nên BE là đường trung tuyến của tam giác ABC, suy ra BE = \(\frac{1}{2}\)AC.
- Ta có O là trung điểm của AC nên AO = OC.
- Ta có I là trung điểm của EC nên EI = IC.
- Ta có tam giác AHE đồng dạng với tam giác AOC (cùng có góc vuông tại A), suy ra \(\frac{AH}{AO}\) = \(\frac{HE}{OC}\).
- Tương tự, ta có tam giác EHI đồng dạng với tam giác ECI, suy ra \(\frac{EH}{EI}\) = \(\frac{EC}{IC}\).
- Kết hợp hai tỷ số trên, ta có \(\frac{AH}{AO}\) = \(\frac{HE}{OC}\) = \(\frac{EH}{EI}\) = \(\frac{EC}{IC\).
- Do đó, ta có tam giác AOI đồng dạng với tam giác EBC (theo định lí đồng dạng), suy ra AO || BE.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515
-
zytera
1325 điểm
-
Dương Nguyễn
960 điểm
-
보고 싶어요
855 điểm
-
돈이없다 💸😭
815 điểm
-
우옌 ✨
790 điểm
-
`d.`
635 điểm
-
`color{blue}text{HuyTùng.`
555 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
540 điểm
-
주디 홉스닉주디🥵👍
520 điểm
-
‧₊˚✩ ₊˚🎧⊹♡≽☁˚˖ִ໋🌷͙֒✧˚.🎀༘⋆⋅♡👾đẹρ-†®åî⋆⭒💫
435 điểm
-
Ngọc Linh hay nói linh tinh
385 điểm
-
Kiều Anh 350 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
345 điểm
-
Bích Hồng 345 điểm
Rút gọn
Bài viết mới nhất Lớp 7
-
2 năm trước4934
