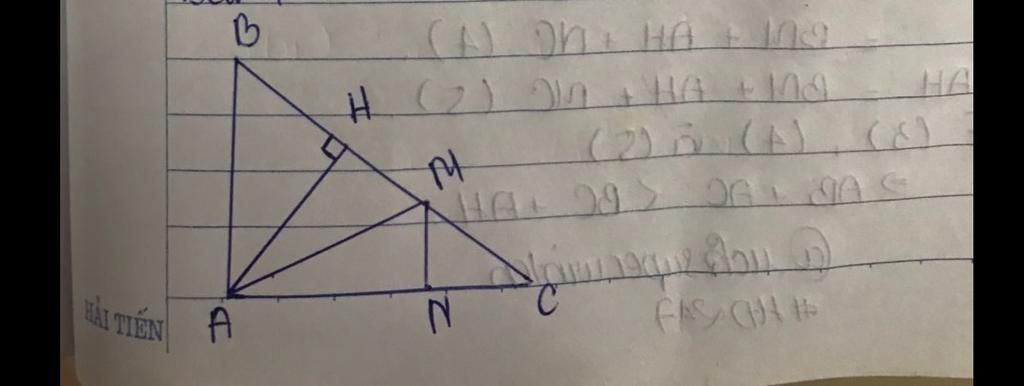Câu 2 (4,0 điểm). Cho tam giác ABC vuông tại A, kẻ AH LBC tại H. Trên các cạnhvà AC lấy tương ứng hai điểm M và N sao cho BM= AB và AN = AH. Chứng minh rằng
a) MN LAC
b) AB+ AC< BC+ AH.
a) MN LAC
b) AB+ AC< BC+ AH.
Quảng cáo
2 câu trả lời 203
a) Ta có BM = AB và AN = AH, từ đó ta có tam giác BMN và tam giác BAH đều vuông tại B. Do đó, ta có:
∠BMN = ∠BAH (cùng bằng 90 độ)
∠MNB = ∠HAB (cùng bằng 90 độ)
Vậy ta có hai góc cạnh trong của hai tam giác BMN và BAH bằng nhau, từ đó suy ra MN // AC (do cặp góc đó bằng nhau).
b) Ta có AB = BM, nên AB = MN. Tương tự, AH = AN, nên AH = MN. Do đó, ta có:
AB + AC = MN + AC > MN
BC + AH = BC + MN > MN
Vậy ta có AB + AC < BC + AH.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669
Gửi báo cáo thành công!