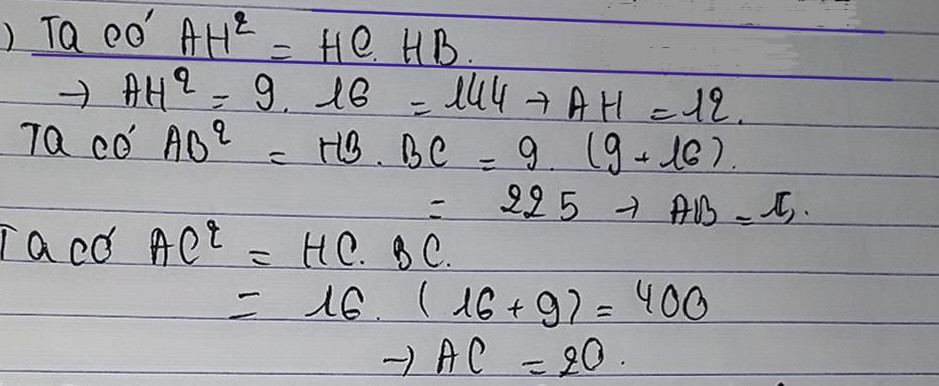Quảng cáo
4 câu trả lời 2966
Để giải bài toán này, ta có thể sử dụng định lý Pythagoras trong tam giác vuông và tính toán theo các thông tin đã cho.
Gọi ( AB = x ), ( AC = y ), ( BC = z ).
Theo định lý Pythagoras trong tam giác vuông ABC, ta có:
[ AB^2 + AC^2 = BC^2 ]
Với AH là đường cao của tam giác ABC, ta có:
[ BH^2 + HC^2 = BC^2 ]
Từ ( BH = 9 ) cm và ( HC = 16 ) cm, ta có:
[ 9^2 + 16^2 = BC^2 ]
[ 81 + 256 = BC^2 ]
[ BC = \sqrt{337} ]
Do đó, ta có hệ phương trình sau:
[ x^2 + y^2 = 337 ] (1)
[ x^2 + (x - 9)^2 = y^2 ] (2)
[ y^2 + (y - 16)^2 = x^2 ] (3)
Giải hệ phương trình (1), (2), (3) để tìm giá trị của ( x ), ( y ), ( z ).
Bạn có thể sử dụng các phần mềm giải phương trình hoặc tính toán thủ công để tìm nghiệm của hệ phương trình trên nhé:))
cho tam giác ABC vuông tại a đường cao AH chiết cạnh huyền thành hai đoạn BH = 9 cm và HC = 16 cm tính AB và ac' BC
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107593
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68300
Đã trả lời bởi chuyên gia
68300 -
 Đã trả lời bởi chuyên gia
52884
Đã trả lời bởi chuyên gia
52884 -
 Đã trả lời bởi chuyên gia
47390
Đã trả lời bởi chuyên gia
47390 -
 Đã trả lời bởi chuyên gia
45461
Đã trả lời bởi chuyên gia
45461 -
 Đã trả lời bởi chuyên gia
45109
Đã trả lời bởi chuyên gia
45109 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38488
Đã trả lời bởi chuyên gia
38488 -
 Đã trả lời bởi chuyên gia
38230
Đã trả lời bởi chuyên gia
38230