Cho tam giác ABC vuông cân tại A. Trên AB, AC lấy D và E sao cho AD = AE. Qua D kẻ đường thẳng vuông góc với BE cắt BC tại I. Qua A kẻ đường thẳng vuông góc với BE cắt BC tại H. Chứng minh rằng: IH = HC.
Quảng cáo
1 câu trả lời 54
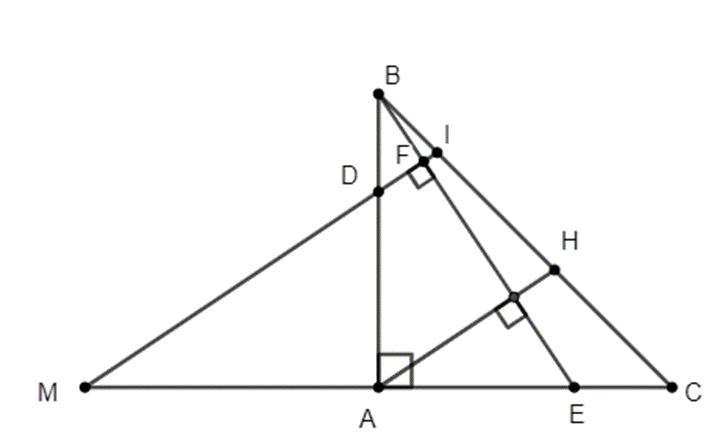
Gọi M là giao điểm của DI và AC. F là giao điểm của DI và BE.
Ta có: \(\widehat {ADM} + \widehat {DMA} = 90^\circ \) (do ∆AND vuông tại A)
\(\widehat {FME} + \widehat {MEF} = 90^\circ \) (Do ∆MFE vuông tại F)
\( \Rightarrow \widehat {DMA} + \widehat {BEA} = 90^\circ \)
\( \Rightarrow \widehat {ADM} = \widehat {BEA}\)
Xét ∆ADM và ∆AEB có:
\(\widehat {ADM} = \widehat {AEB}\)(cmt)
AD = AE (gt)
\(\widehat {DAM} = \widehat {EAB} = 90^\circ \)
Do đó ∆ADM = ∆AEB (g.c.g)
Suy ra AM = AB = AC.
Mà AH // IM (cùng vuông góc BE)
⇒ HA là đường trung bình của ∆ICM
⇒ HI = HC (đpcm).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129704
Đã trả lời bởi chuyên gia
129704 -
 Đã trả lời bởi chuyên gia
104155
Đã trả lời bởi chuyên gia
104155 -
 Đã trả lời bởi chuyên gia
94109
Đã trả lời bởi chuyên gia
94109 -
 Đã trả lời bởi chuyên gia
69540
Đã trả lời bởi chuyên gia
69540



