Quảng cáo
1 câu trả lời 81
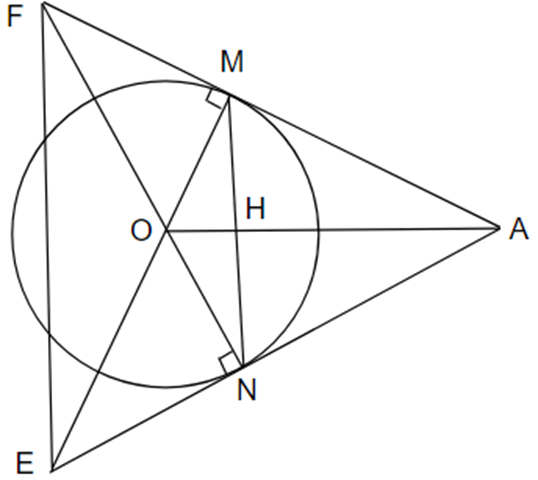
Xét đường tròn (O) có: AM và AN lần lượt là tiếp tuyến tại M và N
Suy ra AM ⊥ OM tại M và AN ⊥ ON tại N
Hay AF ⊥ EM tại M và AE ⊥ FN tại N
Do đó \[\widehat {EMF}\, = \widehat {OMA} = 90^\circ \] và \[\widehat {ENF}\, = 90^\circ \]
Xét tứ giác ENMF có:
\[\widehat {EMF}\, = \widehat {ENF} = 90^\circ \]
Mà 2 đỉnh M và N kề nhau nên tứ giác ENMF nội tiếp.
Suy ra \[\widehat {EFN}\, = \widehat {OMN}\] ( hai góc nội tiếp cùng chắn cung ) (1)
Xét △OMN có:
OM = ON = R nên △OMN cân tại O
Suy ra \[\widehat {OMN} = \widehat {ONM}\,\,\,\,\,\,\,(2)\]
Từ (1) và (2) ta có: \[\widehat {EFN} = \widehat {ONM}\,\,\]
Mà 2 góc này ở vị trí so le trong
Suy ra MN // EF
Vậy MN // EF
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129704
Đã trả lời bởi chuyên gia
129704 -
 Đã trả lời bởi chuyên gia
104155
Đã trả lời bởi chuyên gia
104155 -
 Đã trả lời bởi chuyên gia
94109
Đã trả lời bởi chuyên gia
94109 -
 Đã trả lời bởi chuyên gia
69540
Đã trả lời bởi chuyên gia
69540



