Question

Đã trả lời bởi chuyên gia

Answer 1

Đáp án đúng là: C

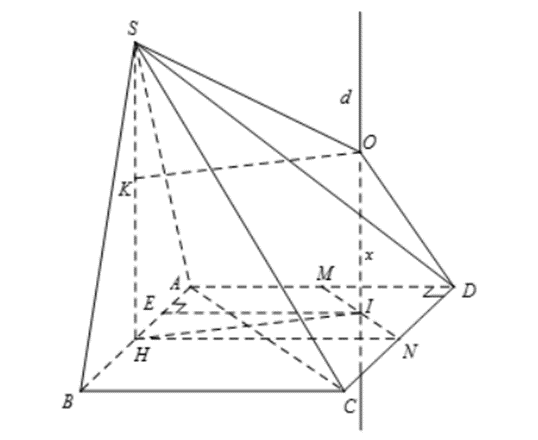
Gọi I là trung điểm của MN. Suy ra I là tâm đường tròn ngoại tiếp tam giác DMN.

d là đường thẳng đi qua I và vuông góc với mặt đáy.

E là hình chiếu của I lên AB.

O là tâm mặt cầu ngoại tiếp tứ diện S.DMN. K là hình chiếu của O lên SH

Đặt OI = x.

Ta có DI = \[\frac{1}{2}MN = \frac{{a\sqrt 5 }}{4}\]. Suy ra:

• \[OD = \sqrt {I{D^2} + O{I^2}} = \sqrt {\frac{{5{a^2}}}{{16}} + {x^2}} \]

• SK = SH - x = \[\frac{{a\sqrt 3 }}{2}\], KO = HI;

• EI = \[\frac{{AM + HN}}{2} = \frac{{3a}}{2}\]

• \[HI = \sqrt {E{I^2} + H{E^2}} = \sqrt {\frac{{9{a^2}}}{4} + \frac{{{a^2}}}{{16}}} = \frac{{a\sqrt {37} }}{4}\]

Do đó \[SO = \sqrt {S{K^2} + K{O^2}} = \sqrt {\frac{{49{a^2}}}{{16}} - a\sqrt 3 x + {x^2}} \]

Vì O là tâm mặt cầu ngoại tiếp nên:

SO = DO Þ \[\frac{{49{a^2}}}{{16}} - a\sqrt 3 x + {x^2} = {x^2} + 5a\]

Þ x = \[\frac{{11a}}{{4\sqrt 3 }}\]Þ R = OD = \[\frac{{a\sqrt {102} }}{6}\].

...Xem thêm

Answer 2