Cho tam giác ABC có \[\widehat B = 90^\circ \], vẽ trung tuyến AM. Trên tia đối của tia MA lấy điểm I sao cho MI = MA.
a) Chứng minh DAMB = DICM.
b) Cho \[\widehat {BAC} = 60^\circ \]. Tính số đo góc ACI.
Quảng cáo
1 câu trả lời 86
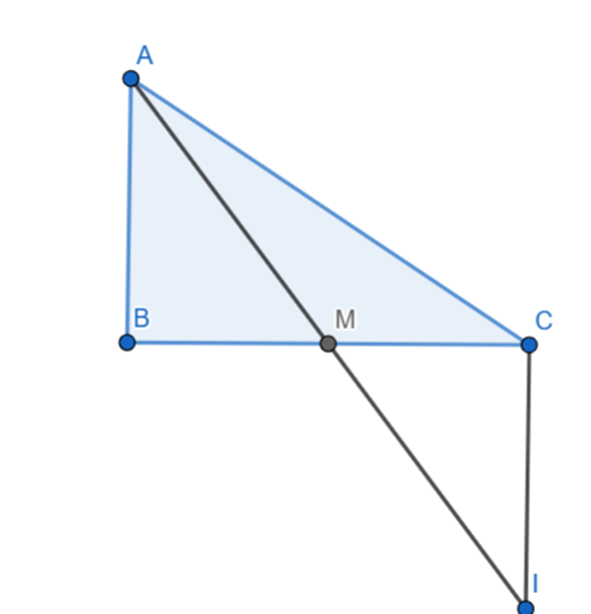
Xét DAMB và DICM có:
AM = IM
\[\widehat {AMI} = \widehat {IMC}\] (đối đỉnh)
MI = MC
Do đó DAMB = DICM (c.g.c).
b) DIMC = DAMB (cmt)
Suy ra \[\widehat {ICB} = \widehat {AIC} = 90^\circ \].
Mà \[\widehat {ACB} + \widehat {BAC} = 90^\circ \] Þ \[\widehat {ACB} = 30^\circ \].
Do đó \[\widehat {ICA} = 120^\circ \].
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129704
Đã trả lời bởi chuyên gia
129704 -
 Đã trả lời bởi chuyên gia
104155
Đã trả lời bởi chuyên gia
104155 -
 Đã trả lời bởi chuyên gia
94109
Đã trả lời bởi chuyên gia
94109 -
 Đã trả lời bởi chuyên gia
69540
Đã trả lời bởi chuyên gia
69540
Gửi báo cáo thành công!



