Cho tam giác ABC có \[\widehat B = 60^\circ \], đường trung tuyến AM, đường cao CH. Vẽ đường tròn ngoại tiếp BHM. Kết luận nào đúng khi nói về các cung HB; MB; MH của đường tròn ngoại tiếp tam giác MHB?
A. Cung HB nhỏ nhất;
B. Cung MB lớn nhất;
C. Cung MH nhỏ nhất;
D. Ba cung bằng nhau.
Quảng cáo
1 câu trả lời 78
Đáp án cần chọn là: D
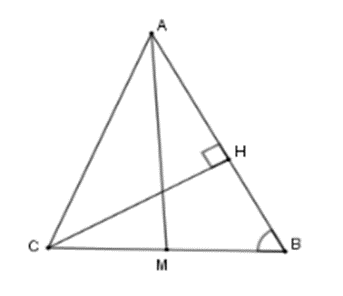
Vì trong một đường tròn hai cung bằng nhau căng hai dây bằng nhau nên ta đi so sánh các đoạn thẳng HB; MB; MH.
Xét tam giác BCH vuông tại H có
\[\cos B = \frac{{HB}}{{BC}} \Leftrightarrow \frac{{HB}}{{BC}} = \cos 60^\circ = \frac{1}{2} \Rightarrow HB = \frac{{BC}}{2} = BM = CM\]
Xét tam giác HBM có BM = BH (cmt) và \[\widehat {ABC} = 60^\circ \] nên DHBM là tam giác đều
Þ BM = BH = HM
Suy ra ba cung HB; MB; MH bằng nhau.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129704
Đã trả lời bởi chuyên gia
129704 -
 Đã trả lời bởi chuyên gia
104155
Đã trả lời bởi chuyên gia
104155 -
 Đã trả lời bởi chuyên gia
94109
Đã trả lời bởi chuyên gia
94109 -
 Đã trả lời bởi chuyên gia
69540
Đã trả lời bởi chuyên gia
69540



