a , chứng minh EF = AH
b , EF cắt AH tại O . Chứng minh OA = OH ,OE = OF
c , chứng minh góc AEF = góc ACB , góc AHE = ABC
Quảng cáo
2 câu trả lời 425
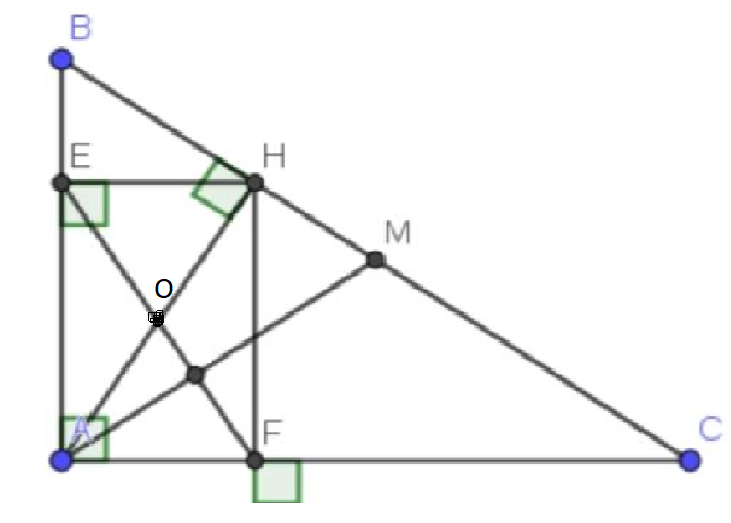
a)
Xét tứ giác AEHF có
Do đó: AEHF là hình chữ nhật
Suy ra: EF=AH
b)
Ta có: AEHF là hình chữ nhật
nên Hai đườg chéo AH và FE cắt nhau tại trung điểm của mỗi đường
hay OA=OH; OE=OF
c,
\( \mathrm{a} \) Để chứng minh \( \mathrm{EF}=\mathrm{AH} \), ta sử dụng các tam giác đồng dạng. Ta có \( \triangle AEF \sim \triangle ACB \) theo nguyên tắc AA (góc - góc). Do đó, tỉ lệ giữa các cạnh của hai tam giác này là bằng nhau. Trong trường hợp này, \( \frac{EF}{AB} = \frac{AE}{AC} \).
Vì \( \triangle ABC \) là tam giác vuông tại \( A \), nên \( AB \) là cạnh huyền. Khi đó, \( AC \) là cạnh góc. Ta có \( AE = AB - BE \) và \( AC = AH + HC \).
Thay các giá trị này vào phương trình trên, ta được:
\[ \frac{EF}{AB} = \frac{AB - BE}{AH + HC} \]
Tuy nhiên, \( BE = HC \) (vì \( BE \) và \( HC \) là chiều cao của tam giác \( ABE \) và \( AHC \) tương ứng). Do đó,
\[ \frac{EF}{AB} = \frac{AB - HC}{AH + HC} \]
Nhưng \( AB = AH + HC \) (theo định lý Pythagoras trong tam giác vuông), nên:
\[ \frac{EF}{AB} = \frac{AB - HC}{AB} \]
\[ EF = AB - HC \]
\[ EF = AH \]
Do đó, \( EF = AH \).
\( \mathrm{b} \) Để chứng minh \( \mathrm{OA}=\mathrm{OH} \) và \( \mathrm{OE}=\mathrm{OF} \), ta sử dụng tính chất của các tam giác đồng dạng và tam giác vuông.
Gọi \( O \) là giao điểm của \( EF \) và \( AH \).
Trong tam giác \( AEF \) và \( ACB \), ta có \( \triangle AEF \sim \triangle ACB \) theo AA (góc - góc). Do đó, \( \frac{EF}{AB} = \frac{AE}{AC} \).
Gọi \( x \) là độ dài của \( EF \), \( y \) là độ dài của \( AH \), \( z \) là độ dài của \( AO \).
\( \frac{x}{AB} = \frac{AE}{AC} \) (1)
Vì \( AE = AB - BE \) và \( AC = AH + HC \), thay giá trị vào (1), ta được:
\[ \frac{x}{AB} = \frac{AB - BE}{AH + HC} \]
Tương tự như ở \( \mathrm{a} \), \( BE = HC \), \( AB = AH + HC \), nên:
\[ \frac{x}{AB} = \frac{AB - HC}{AB} \]
\[ \frac{x}{AB} = \frac{AH}{AB} \]
\[ x = AH \]
Do đó, \( EF = AH \).
Tiếp theo, ta chứng minh \( OA = OH \) và \( OE = OF \).
Trong tam giác \( AOE \) và \( AOF \), ta có \( \angle AOE = \angle AOF \) (vì \( EF \) là đường chia đều góc \( AOH \)). Ta cũng có \( \angle OAE = \angle OAF \) (vì \( AO \) là đường chia đều góc \( EAF \)).
Do đó, \( \triangle AOE \) và \( \triangle AOF \) là các tam giác đồng dạng theo AA (góc - góc). Từ đó, \( \frac{OA}{OE} = \frac{OH}{OF} \).
Nhưng \( OH = OA + AH \) (vì \( O \) là giao điểm của \( EF \) và \( AH \)).
Thay giá trị vào phương trình trên:
\[ \frac{OA}{OE} = \frac{OA + AH}{OF} \]
\[ OA \cdot OF = OA \cdot OE + AH \cdot OA \]
\[ OA \cdot (OF - OE) = AH \cdot OA \]
\[ OA = AH \]
Do đó, \( OA = OH \) và \( OE = OF \).
\( \mathrm{c} \) Để chứng minh \( \angle AEF = \angle ACB \) và \( \angle AHE = \angle ABC \), ta sử dụng tính chất của các tam giác đồng dạng.
Trong tam giác \( AEF \) và \( ACB \), ta đã chứng minh \( \triangle AEF \sim \triangle ACB \) (theo \( \mathrm{a} \)). Do đó, \( \angle AEF = \angle ACB \).
Trong tam giác \( AHE \) và \( ABC \), ta cũng có \( \triangle AHE \sim \triangle ABC \) theo AA (góc - góc). Do đó, \( \angle AHE = \angle ABC \).
Như vậy, \( \angle AEF = \angle ACB \) và \( \angle AHE = \angle ABC \) đã được chứng minh.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


