Cho ∆ABC vuông tại A (AB < AC) có đường cao AH (H thuộc BC) và phân giác BD
của góc ABC (D thuộc AC )
a) Chứng minh: ∆BAH đồng dạng ∆BCA và góc BAH bằng góc BCA
b) Gọi I là giao điểm của AH và BD. Chứng minh: BI. BC=BA.BD .
c) Kẻ CE L BD cắt tia BA tại M. Chứng minh: AI // MD và BA.BM +CE.CM = BC^2.
Nam Thanvannam
· 1 năm trước
Phânt c làm kiểu gì
Quảng cáo
1 câu trả lời 3054
2 năm trước
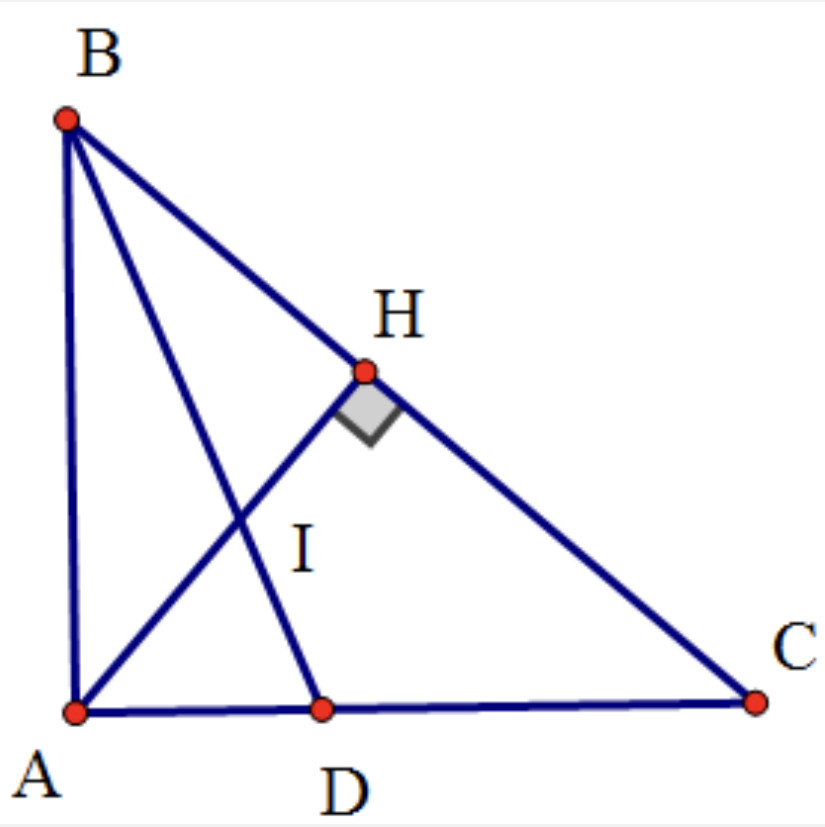
a)
Xét ΔHBA và ΔABC có:
g.H = g.A =90 độ (gt)
g.B chung
=> ΔHBA ~ΔABC (g.g)
=> góc BAH = góc BCA
b)
Xét ΔABI và ΔCBD có:
góc ABI = góc CBD (do BD là phân giác)
góc BAI = góc BCD (cùng phụ với góc HAC)
=> ΔABI ~ΔCBD (g.g)
=> BI/BD = BA/BC
=> BI.BC = BA.BD
nguyen minh chau
· 2 năm trước
ko co cau C ak chij
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
4043
Gửi báo cáo thành công!


