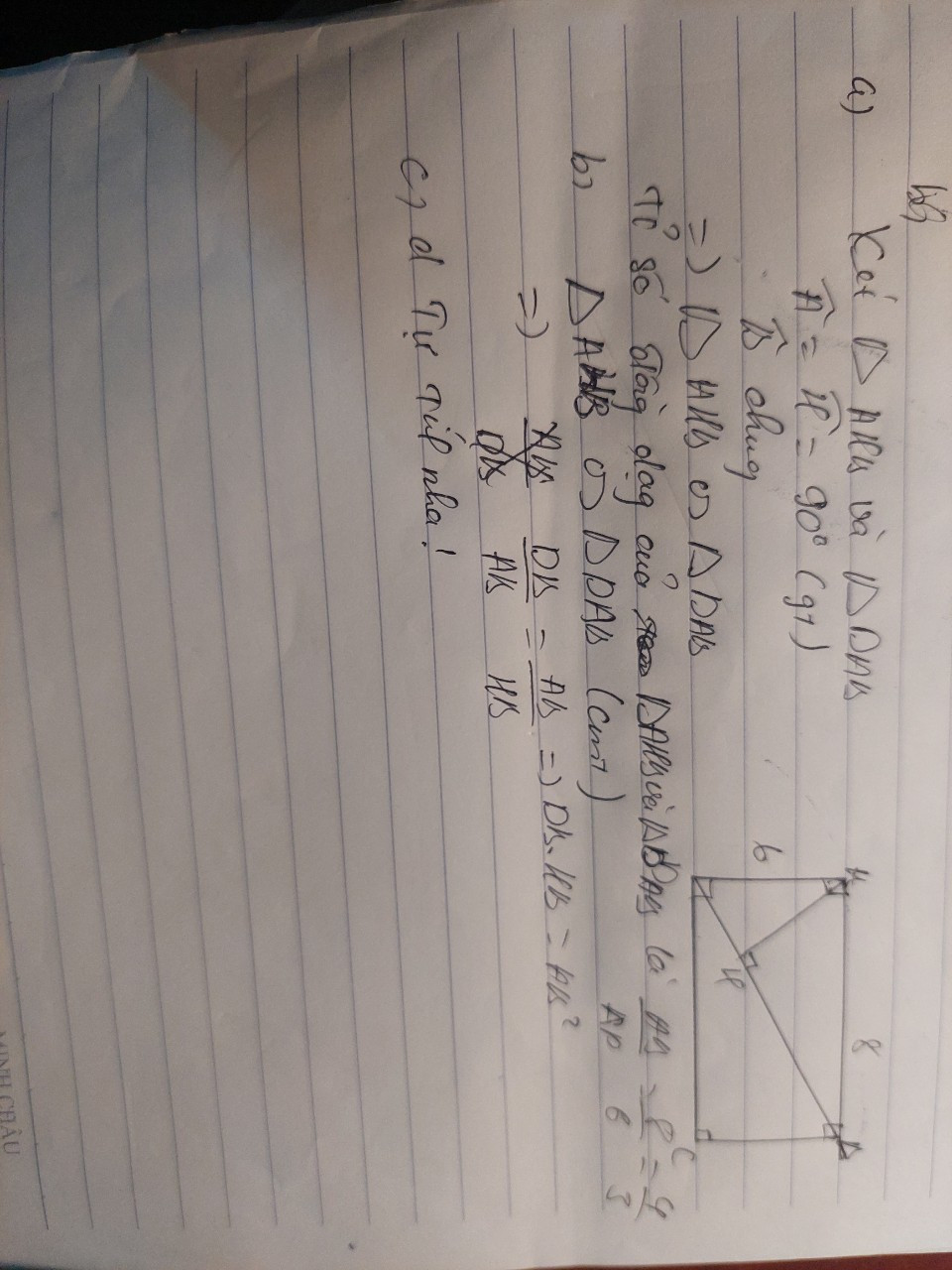a) Ta có:

Góc AHB và góc DAB là góc vuông (do AB và AD là hai cạnh của hình chữ nhật ABCD).
Góc HAB và góc ADB là góc nhọn bù (do AH là đường cao của tam giác ABD).
Vậy nên ∆AHB đồng dạng với ∆DAB theo góc góc góc.
Tỉ số đồng dạng giữa ∆AHB và ∆DAB là: AB/AD = 8/6 = 4/3.
b) Ta có:

Góc AHB và góc DAB là góc vuông (do AB và AD là hai cạnh của hình chữ nhật ABCD).
Vậy nên ∆AHB và ∆DAB có một góc bằng nhau.
Theo định lí Euclid, trong tam giác vuông, đường cao bằng tích của cạnh huyền với phần dư của cạnh kề đối góc vuông cho đường cao.
Áp dụng định lí Euclid cho tam giác ABD, ta có: AH² = BD × HD.
Vì BD = AB = 8cm và HD = AD - AH = 6 - AH, nên ta có: AH² = 8(6 - AH).
Giải phương trình trên, ta được: AH = 24/5 cm.
c) Diện tích tam giác AHB là:

S(∆AHB) = (1/2) × AB × AH = (1/2) × 8 × (24/5) = 96/5 cm².

ới tam giác CEB. Từ đó suy ra: góc BCF bằng góc CBE. Vậy nên hai cặp đường thẳng BF và CE, BC và FE lần lượt song song với nhau (do các góc tương ứng bằng nhau). Từ đó suy ra Be song song với CF.

Để chứng minh AD là đường cao của tam giác AFC, ta có:

Vì BD là tia phân giác của góc A, nên góc ABD bằng góc CBD.
Từ BF = CE, suy ra tam giác BFC đồng dạng với tam giác CEB.
Từ đó suy ra: góc BCF bằng góc CBE.
Vậy nên tam giác BCF đồng dạng với tam giác CBE.
Từ tam giác BDF đồng dạng với tam giác CEF, suy ra góc BFD bằng góc CFE.
Vậy nên tam giác BFD đồng dạng với tam giác CFE.
Từ đó suy ra: góc BDF bằng góc CEF.
Vì BD = DC (do BD là tia phân giác của góc A), nên tam giác BDC là tam giác đều.
Từ đó suy ra: góc BDC bằng 60 độ.
Vậy nên góc ADB bằng 30 độ.
Vì góc AFC bằng 90 độ (do AF là đường cao của tam giác), nên góc AFB bằng 60 độ.
Từ đó suy ra: góc AFD bằng 30 độ.
Vậy nên AD song song với BF (do cùng bằng 30 độ).
Nhưng BF song song với CE, nên AD cũng song song với CE.
Vậy nên AD là đường cao của tam giác AFC.