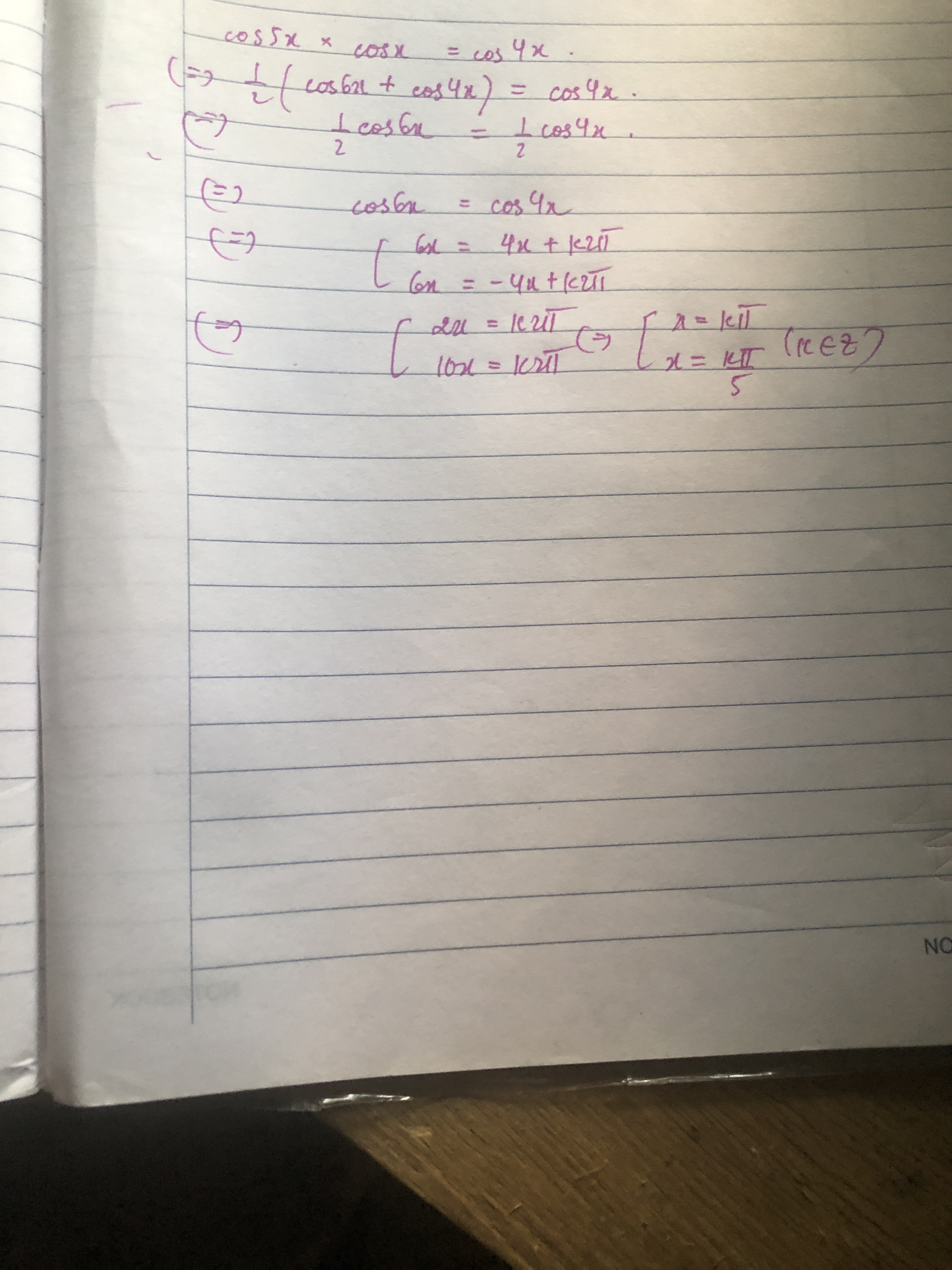Quảng cáo
3 câu trả lời 815
áp dụng công thức $cosa+cosb=2cos\frac{a+b}{2}cos\frac{a-b}{2}$
ta có $cos5x.cosx=\frac{1}{2}cos\frac{6x+4x}{2}cos\frac{6x-4x}{2}$
PT $⇔\frac{1}{2}cos6x+\frac{1}{2}cos4x=cos4x$
$⇔\frac{1}{2}cos6x-\frac{1}{2}cos4x=0$
$⇔cos6x-cos4x=0$
$⇔cos6x=cos4x$
⇔\(\left[ \begin{array}{l}6x=4x+k2\pi\\6x=-4x+k2\pi\end{array} \right.\)⇔ \(\left[ \begin{array}{l}2x=k2\pi\\10x=k2\pi\end{array} \right.\) ⇔\(\left[ \begin{array}{l}x=k\pi\\x=k\frac{\pi}{5}\end{array} \right.\) $(k∈Z)$
Áp dụng công thức biến tích thành tổng ta có
(1/2)(cos(6x)+cos(4x))=cos(4x)(1/2)(cos(6x)+cos(4x))=cos(4x)
<->(1/2)cos(6x)=(1/2)cos(4x)(1/2)cos(6x)=(1/2)cos(4x)
<->cos(6x)=cos(4x)cos(6x)=cos(4x)
<->6x=4x+2kπ6x=4x+2kπ hoặc 6x=−4x+2kπ6x=−4x+2kπ
<-> x=kπx=kπ hoặc x=kπ/5x=kπ/5.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
134838
Đã trả lời bởi chuyên gia
134838 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
75920
Đã trả lời bởi chuyên gia
75920 -
 Đã trả lời bởi chuyên gia
71641
Đã trả lời bởi chuyên gia
71641 -
 Đã trả lời bởi chuyên gia
47575
Đã trả lời bởi chuyên gia
47575