Quảng cáo
2 câu trả lời 789
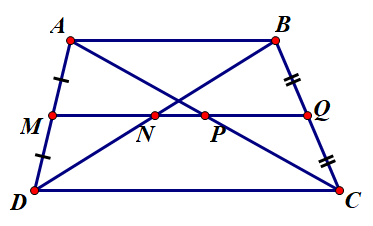
Ta có:
AM=MD (M là trung điểm AD)
BQ=QC ( Q là trung điểm BC)
nên MQ là đường trung bình của hình thang ABCD
⇒MQ//AB (1)
Tương tự:
Xét tam giác ABD:
- M là trung điểm AD
- N là trung điểm BD
nên MN là đường trung bình của tam giác ABD
⇒MN//AB (2)
Xét tam giác ABC:
- P là trung điểm AC
- Q là trung điểm BC
nên PQ là đường trung bình của tam giác ABC
⇒MN //AB. (3)
Từ (1)(2)(3)
⇒MN;MQ;PQ trùng nhau
hay M,N,P,Q thẳng hàng (đpcm)
Xét hình thang ABCD(AB//CD) có : NB=NC; MD=MA
MN là đường trung bình hình thang ABCD
MN//AB
Ta có: BCA có NB=NC; PC=PA
NP là đường trung bình của BCA
NP//CD
NP//AB (vì AB//CD)
Ta có: CDA có MD=MA; PC=PA
MP là đường trung bình của CDA
MP//CD MP//AB
Từ(1); (2) ;(3) M,N,P thẳng hàng(*)
Ta có: △CDB có QD=QB; NC=NB
⇒ NQ là đường trung bình của △CDB
⇒ NQ//CD ⇒ NQ//AB(4)
Ta có: △ADB có QD=QB ; MD=MA
⇒ MQ là đường trung bình của △ADB
⇒ MQ//CD ⇒ MQ//AB(4)
Từ(1), (3), (4) ⇒ N,Q,M thẳng hàng (**)
Từ(*); (**) ⇒⇒ N,Q,P,M thẳng hàng
b. Ta có: NM là đường trung bình hình thang ABCD
Ta có NQ và MP là đưởng trung bình của △CDB và △CDA
Ta lại có:
Hay
⇔
⇒
c) Ta có: MP=PQ=QN
⇔y2=x−y2
⇔y2=x−y+y4 (Tính chất dãy tỉ số bằng nhau)
Quảng cáo
Câu hỏi hot cùng chủ đề
-
102548
-
Hỏi từ APP VIETJACK55466
-
Cho tam giác MNP vuông tại M,đường cao MH
a, Chứng minh tam giác HMN đồng dạng với tam giác MNP
b, chứng minh hệ thức MH2=NH.PH
c, Lấy điểm E tùy ý trên cạnh MP,vẽ điểm F trên cạnh MN sao cho góc FHE =90 độ. Chứng minh tam giác NFH đồng dạng với tam giác MEH và góc NMH=góc FEH
d,Xác định vị trí điểm E trên MP sao cho diện tích tam giác HEF đạt giá trị nhỏ nhất
43543












