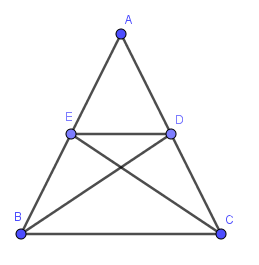
7. (Dạng 3). Cho tam giác ABC cân tại A, các đường phân giác BD CE , .
a) Tứ giác BEDC là hình gì? Vì sao?
b) Tính chu vi tứ giác BEDC , biết BC cm ED cm = = 15 , 9
Quảng cáo
2 câu trả lời 1303
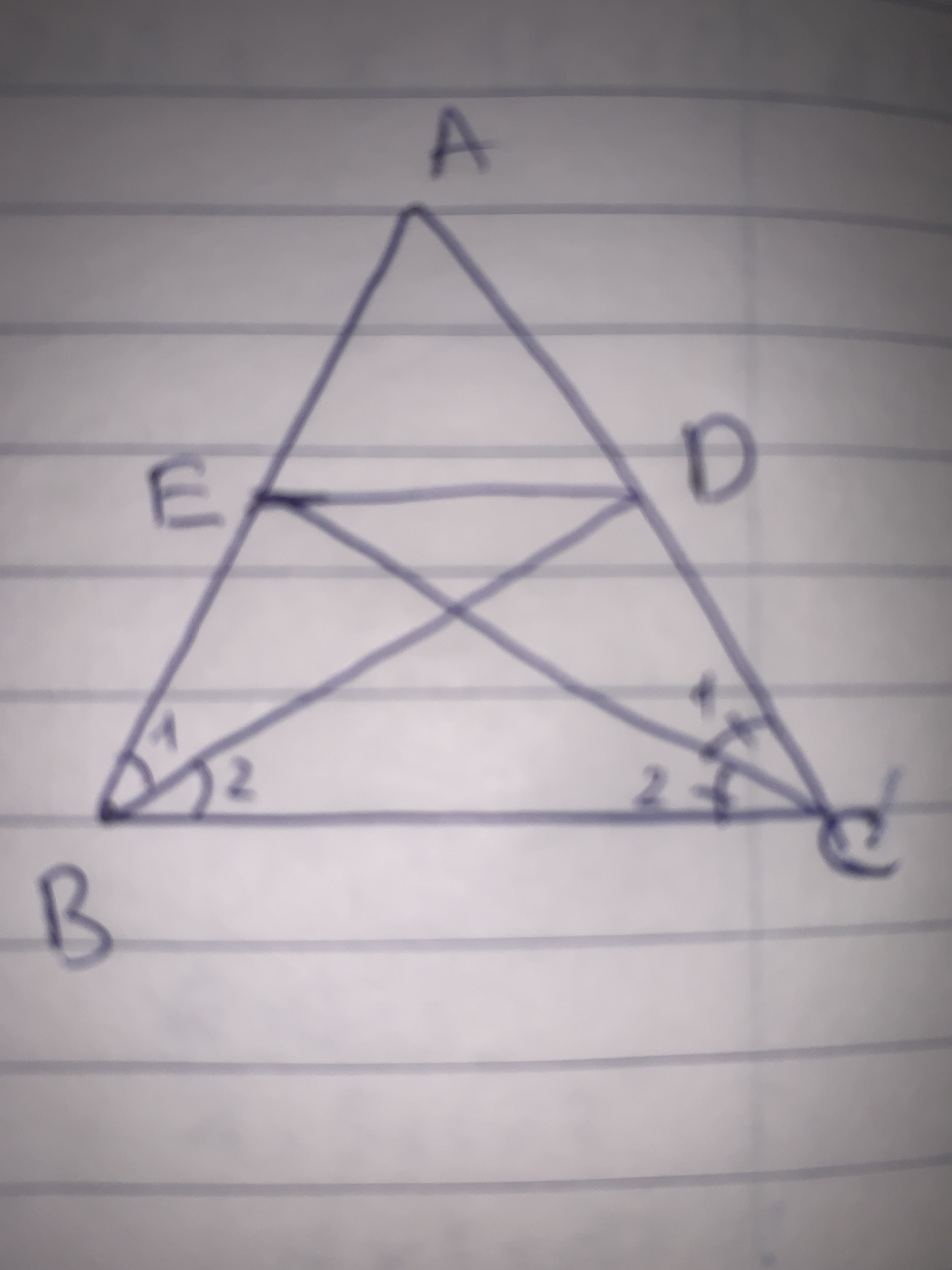
a. Theo tính chất tia phân giác, do BD, CE lần lượt là phân giác của góc B và góc C nên:
AD/DC=AB/BC
AE/EB=AC/BC
Mà AB=AC (do tam giác ABCcân)
⇒AD/DC=AE/EB
⇒ED // BC (theo định lý Talet)
⇒BEDC là hình thang
Mà 2 góc ở đáy là góc B và góc C bằng nhau (do ABC cân tại A)
⇒BEDC là hình thang cân.
b.
Ta có:
góc EDB=góc DBC (so le trong)
Mà góc DBC= góc EBD (do BD là phân giác góc B )
⇒ góc EDB= góc EBD
⇒EBD là tam giác cân tại E
⇒EB=ED=9 (cm)
BEDC là hình thang cân nên
DC=EB=9(cm)
Do đó:
Chu vi của BEDC là:
ED+EB+DC+BC=9+9+9+15=42(cm)
Quảng cáo
Bạn muốn hỏi bài tập?