Cho `m,n\in RR` thỏa mãn pt: `x^3+mx^2+nx+1=0` luôn có `3` nghiệm `a,b,c` phân biệt. CMR: `\sqrt2/a+\sqrt3/b-\sqrt(2+\sqrt3)/c<=a^2+b^2+c^2`
đố ai làm đc câu này :))
Quảng cáo
2 câu trả lời 346
3 năm trước
f(x)=x3+mx2+nx−1f(0)=−1<0f(1)=m+n>0f(2)=7+2(2m+n)<0f′(x)=3x2+2mx+nΔ′=m2−3n
Các số f(0),f(1),f(2) thay đổi tính âm dương nên hàm số phải có 3 nghiệm
Ta có các bảng biến thiên sau:
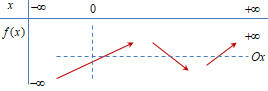
Chỗ x=0 không thể là cực trị do f′(0)=n≠0, vì nếu n=0 thế vào điều kiện ban đầu ta có {m>07+4m<0 (vô lí).
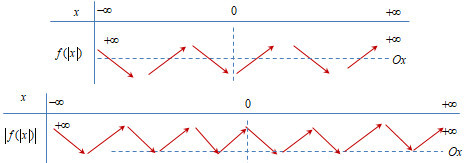
Hàm số y=|f(|x|)| có 11 điểm cực trị.
Anh Tham Khảo Ạ
$\Huge\color{white}{\text{.}}$
· 3 năm trước
.....
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
Gửi báo cáo thành công!



