a) Chứng minh rằng tam giác HBA đồng dạng tam giác ABC
b) Tính các đoạn thẳng BC , AH , BH và CH
Quảng cáo
3 câu trả lời 3541
Xét tam giác vuông HBA và tam giác vuông ABC có :
Chung góc B
=> tam giác HBA đồng dạng tam giác ABC (g,g) (1)
=> AC.BC=BA.AH
Xét tam giác vuông ABC có :
=> 20.25= 15.AH
=> AH=33,33 cm
Từ (1) =>
Có BC = HC + HB
=> 25 = 9 + HC => HC= 25 - 9 = 16 CM
a)Vì `AH` là đường cao của `ΔABC`
`=>` $\widehat{AHB}$=90
Xét `ΔHBA` và `ΔABC` có :
$\widehat{AHB}$=$\widehat{BAC}$=90
$\widehat{ABH}$ góc chung
`=>``ΔHAB`~`ΔABC` (g.g)
b) VìΔ`ABC` vuông tại `A`
`=>` `BC^2=AB^2+AC^2` ( định lý Py-ta-go)
`=>` `BC^2=15^2+20^2=625`
`=>` `BC=25(cm)`
Vì`ΔHAB`~`ΔABC` (cmt)
`=>` (AH)/(AB)=(AB)/(BC)
`=>` `AH=(AB^2)/(BC)=15^2/25=9(cm)`
Vì`ΔHAB`~`ΔABC` (cmt)
`=>` (BH)/(AB)=(AC)/(BC)`
`=>` `BH=(AB.AC)/BC=12(cm)`
Có `AC=BH+CH`
`=>` `CH=AC-BH=20-12=8(cm)`
Vậy : `BC=25cm,AH=9cm;BH=12cm;CH=8cm`
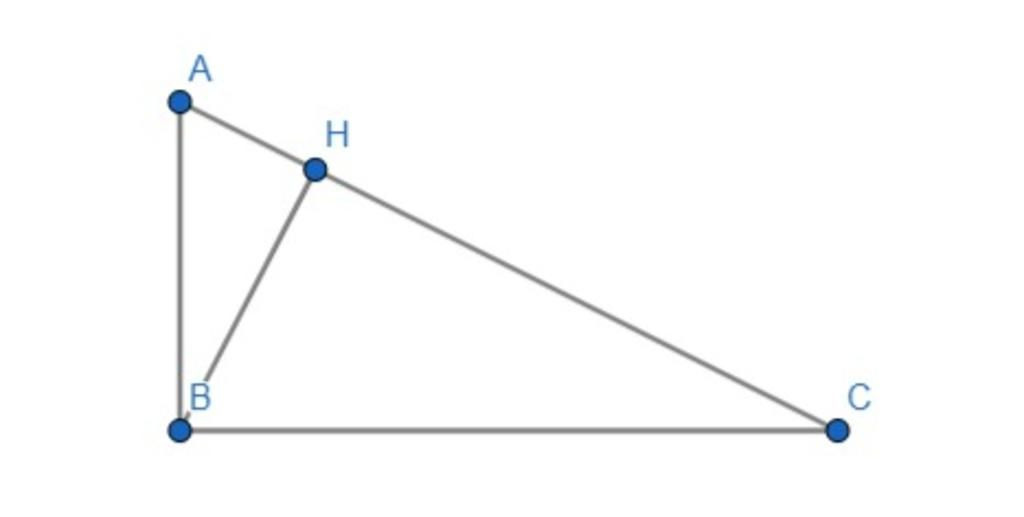
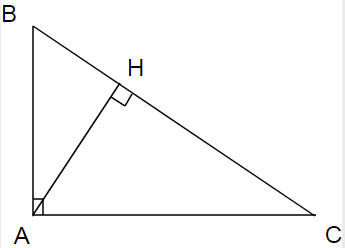
a) Xét tam giác HBA và tam giác ABC :
Góc AHB = góc BAC(=90 độ )
Góc ABC:chung
=> tam giác HBA đồng dạng tam giác ABC ( đpcm )
b) Áp dụng đính lý Pytago vào tam giác ABC vuông tại A
Từ câu b) ta có :
Mà BH=BC-HC => BH=25-16 =9 (cm)
Áp dụng định lý Pytago trong tam giác AHC vuông tại H có:
Vậy BC=25cm; AH=12cm; BH= 9cm; CH= 16cm
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171


