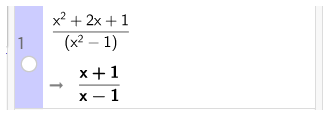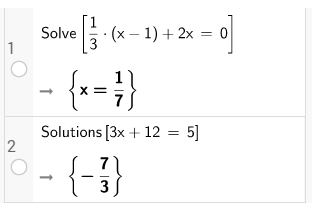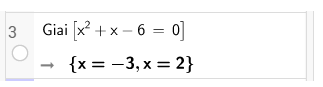Tin học 8 Bài 11: Giải toán và vẽ hình phẳng với GeoGebra
Lý thuyết tổng hợp Tin học 8 Bài 11: Giải toán và vẽ hình phẳng với GeoGebra chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Tin 8. Hy vọng bộ tổng hợp lý thuyết Tin học lớp 8 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Tin học 8.
Bài 11: Giải toán và vẽ hình phẳng với GeoGebra
A. Lý thuyêt
• Nội dung chính
- Tính toán với đa thức, phân thức đại số, giải phương trình và bất phương trình bậc nhất 1 ẩn với GeoGebra.
- Vẽ hình phẳng theo nội dung hình học 8.
1. Các phép tính trên đa thức
- Sử dụng chế độ tính toán chính xác trên cửa sổ CAS.
- Một số lệnh làm việc chính với đa thức;
| Cú pháp lệnh | Ý nghĩa |
| Factor[<đa thức>] | Khai triển đa thức thành tích các thừa số trong phạm vi các số hữu tỉ |
| iFactor[<đa thức>] | Khai triển đa thức thành tích các thừa số trong phạm vi các số vô tỉ |
| Expand[<đa thức>] | Khai triển biểu thức tính toán đa thức |
| Simplify[<đa thức>] | Rút gọn biểu thức tính toán đa thức |
| Div[<đa thức1>,<đa thức 2>] | Cho thương của phép chia đa thức 1 cho đa thức 2 |
| Mod[<đa thức1>,<đa thức 2>] | Cho số dư của phép chia đa thức 1 cho đa thức 2 |
| Division[<đa thức1>,<đa thức 2>] | Cho thương và số dư của phép chia đa thức 1 cho đa thức 2. |
- Ví dụ:
2. Các phép tính trên phân thức đại số
- Nhập trực tiếp phân thức cần tính toán trên dòng lệnh cửa sổ CAS
- Phần mềm sẽ tự động tính toán và rút gọn phân thức nếu được.
- Ví dụ:
3. Giải phương trình và bất phương trình bậc nhất 1 ẩn
- Sử dụng các lệnh để giải phương trình và bất phương trình
- Cú pháp:
+ Solve[< phương trình x>] hoặc Solve[< bất phương trình x>] cho kết quả là các nghiệm của phương trình hoặc bất phương trình
+ Solutions[< phương trình x>]
hoặc Solutions[< bất phương trình x>] cho kết quả là tất cả các giá trị nghiệm của phương trình, bất phương trình.
- Ví dụ:
- 2 câu lệnh trên cũng có thể được dùng để giải các phương trình bậc cao hơn.
4. Quan hệ toán học và các công cụ tạo quan hệ toán học trong GeoGebra
- Tất cả các công cụ( đại số và hình học) của GeoGebra đều có chức năng chính là thiết lập các đối tượng toán học thông qua các quan hệ toán học.
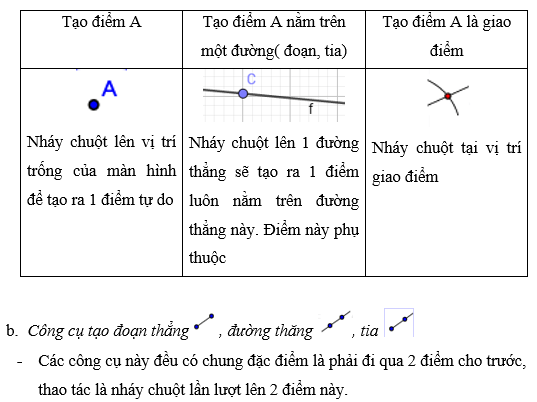
a) Công cụ tạo điểm
- Chọn công cụ tạo điểm
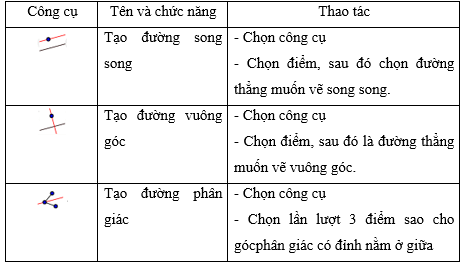
c. Công cụ vẽ các đường song song, phân giác, vuông góc, trung trực
d. Tạo đối tượng số trực tiếp từ dòng lệnh
- Tạo ra đối tượng số tự do từ ngay dòng lệnh bằng cách nhập vào dòng lệnh như sau: a:= 1.
- Phần mềm sẽ tạo ra 1 đối tượng số tự do có tên là a, giá trị bằng 1. Bây giờ chúng ta tạo ra các đối tượng khác phụ thuộc vào a.
- Ví dụ: b:=a/2; c:=a2.
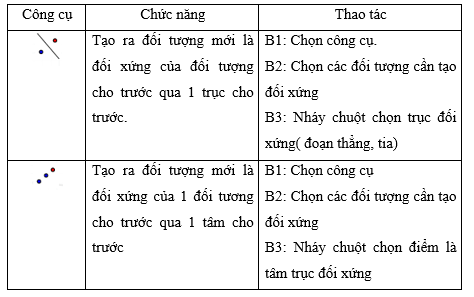
5. Các công cụ biến đổi hình học
- 2 công cụ chính:
+ Lấy đối xứng trục
+ Lấy đối xứng tâm
a) Vẽ hình thang cân biết cạnh đáy và 1 cạnh bên
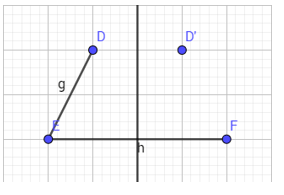
- B1: vẽ cạnh đáy và 1 cạnh bên
- B2: vẽ đường trung trực cho cạnh đáy
- B3: tạo điểm đối xứng của điểm D qua đường trung trực, ta được D′
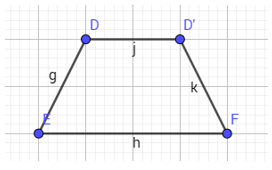
- B4: nối D với D′, F với D′ và ẩn đường trung trực
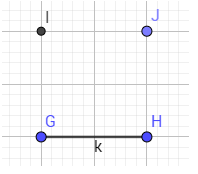
b. Vẽ hình bình hành, biết 1 cạnh và tâm
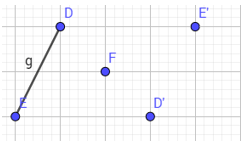
- B1: vẽ 1 cạnh và 1 tâm
- B2: lấy đối xứng 2 điểm đầu và cuối của cạnh trên qua tâm
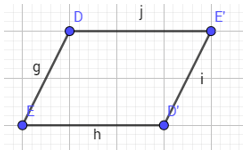
- B3: nối các điểm lại với nhau và ẩn tâm đi.
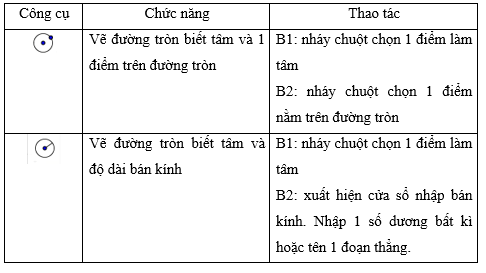
6. Công cụ đường tròn và cách vẽ 1 số hình đặc biệt
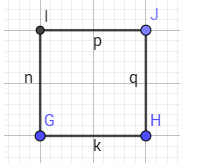
a) Vẽ hình vuông biết 1 cạnh
- B1: vẽ đoạn thẳng là cạnh cho trước của hình vuông
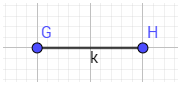
- B2: Sử dụng công cụ đường vuông góc vẽ 2 đường thẳng vuông góc với đoạn thẳng đã cho và đi qua 2 điểm đầu mút.
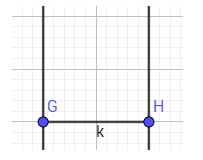
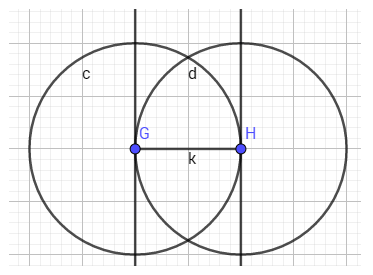
- B3: sử dụng công cụ vẽ đường tròn lấy 2 điểm đầu mút làm tâm vẽ và đường tròn đi qua đỉnh còn lại
- B4: xác định giao điểm, sau đó ẩn 2 đường tròn và 2 đường vuông góc đi
- B5: nối 4 điểm lại với nhau để thành hình vuông.
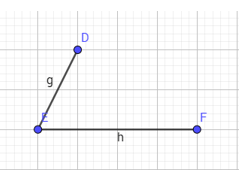
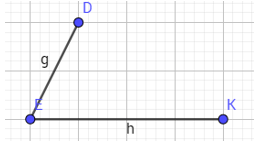
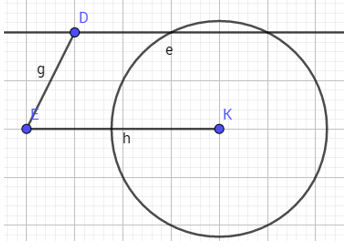
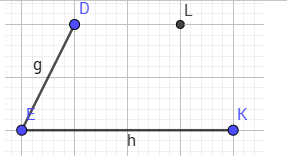
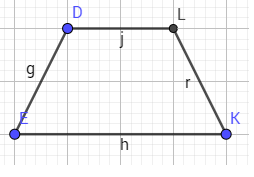
b. Vẽ hình thang cân biết trước 1 cạnh đáy và 1 cạnh bên
- B1: cho trước 2 cạnh của hình thang cân với 3 đỉnh tự do
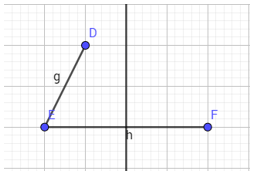
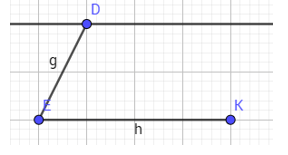
- B2: vẽ đường song song từ 1 đỉnh trên( D) với cạnh đáy(EK)
- B3: dùng công cụ vẽ đường tròn vẽ 1 đường tròn có tâm là đỉnh ở đáy (K) và bán kính bằng độ dài cạnh bên(ED = g)
- B4: xác định giao điểm của đường tròn và đường thẳng kẻ song song.
- B5: ẩn các đường không cần thiết, nối các điểm lại với nhau.
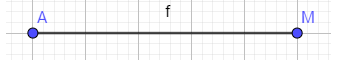
c. Chia 3 một đoạn thẳng
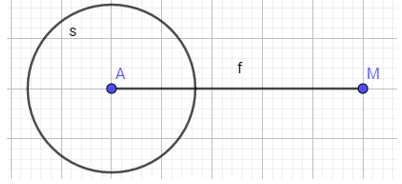
- B1: vẽ 1 đoạn thẳng AM
- B2: vẽ đường tròn có tâm là đỉnh bên trái( A) và bán kính là AM/3 = f/3
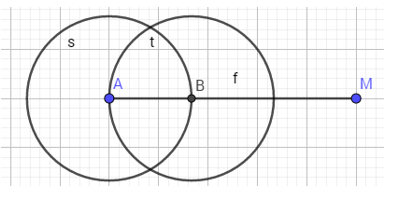
- B3: vẽ đường tròn mới với tâm( B) là giao điểm của đường tròn vừa nãy( đường tròn s) với đoạn AM, và đường tròn mới( t) đi qua điểm bên trái(A)
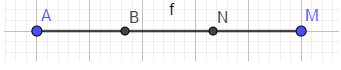
- B4: xác định giao điểm mới( N). và ẩn các đường không cần thiết ta sẽ có đoạn thẳng được chia làm 3 phần bằng nhau.

B. Bài tập trắc nghiệm
Câu 1:Màn hình làm việc chính của phần mềm GeoGebra gồm:
A. Bảng chọn
B. Thanh công cụ
C. Khu vực thể hiện các đối tượng
D. Tất cả ý trên
Màn hình làm việc chính của phần mềm GeoGebra gồm: Bảng chọn, thanh công cụ, khu vực thể hiện các đối tượng.
Đáp án: D
Câu 2:phần mềm GeoGebra là phần mềm:
A. Giúp luyện gõ bàn phím nhanh và chính xác
B. Giúp vẽ hình chính xác
C. Có khả năng vẽ hình học động
D. Cả B và C
phần mềm GeoGebra là phần mềm giúp vẽ hình chính xác và có khả năng vẽ hình học động, hình không gian.
Đáp án: D
Câu 3:Để thoát khỏi phần mềm, em chọn cách nào sau đây?
A. File -> Exit
B. Alt + F4
C. Hồ sơ -> Đóng
D. Cả B và C đều được
Để thoát khỏi phần mềm ta nhấn tổ hợp phím Alt + F4 hoặc Hồ sơ -> Đóng.
Đáp án: D
Câu 4:ta có:
B1: vẽ 1 cạnh và 1 tâm
B2: ẩn tâm đi.
B3: nối các điểm lại với nhau.
B4: lấy đối xứng 2 điểm đầu và cuối của cạnh trên qua tâm
Để vẽ hình bình hành, biết 1 cạnh và tâm ta thực hiện như thế nào?
A. B1 – B4 – B2 – B3
B. B1 – B4 – B3 – B2
C. B2- B3 – B4 – B1
D. B1- B2- B4 – B3
Để vẽ hình bình hành, biết 1 cạnh và tâm ta thực hiện:
B1: vẽ 1 cạnh và 1 tâm
B2: lấy đối xứng 2 điểm đầu và cuối của cạnh trên qua tâm
B3: nối các điểm lại với nhau.
B4: ẩn tâm đi.
Đáp án: B
Câu 5:Để hiển thị lưới ở khu vực vẽ hình em thực hiện thao tác nào?
A. Tùy chọn -> Lưới
B. Hiển thị -> Lưới
C. Công cụ -> Lưới
D. Cửa sổ -> Lưới
Để hiển thị lưới ở khu vực vẽ hình ta thực hiện chọn Hiển thị -> Lưới.
Đáp án: B
Câu 6:Trong phần mềm GeoGebra, khi gõ lệnh Slove [ 2x – 2=0] kết quả đưa ra là gì?
A. { x= 2}
B. { x = 1}
C. { x=3 }
D. {x =4}
Cú pháp: Solve[< phương trình x>] hoặc Solve[< bất phương trình x>] cho kết quả là các nghiệm của phương trình hoặc bất phương trình. Nên nghiệm của phương trình 2x- 2= 0 → x =1.
Đáp án: B
Câu 7:Kết quả của lệnh Expand [(x-3)2] là
A. X2 – 6x +9
B. X3 + 6 x + 9
C. X2 + 6x +9
D. (x -2) (x +2)
Lệnh Expand[<đa thức>] là lệnh khai triển biểu thức tính toán đa thức.
Đáp án: A
Câu 8:Kết quả của câu lệnh Mod[ x2 + 2, x +1] là:
A. 1
B. -1
C. 3
D. 0
lệnh Mod[<đa thức1>,<đa thức 2>] là cho số dư của phép chia đa thức 1 cho đa thức 2. Mà (x2 + 2) : (x+1 ) = x-1 và dư 3
Đáp án: C