cho hình bình hành ABCD và O là giao điểm của AC và BD . Trên đường chéo AC lấy 2 điểm M và N sao cho AM = MN = NC
a) CM : tứ giác BMDN là hình bình hành
b) BC cắt DN tại K . CM : N là trọng tâm của tam giác BDC
Quảng cáo
3 câu trả lời 575
2 năm trước
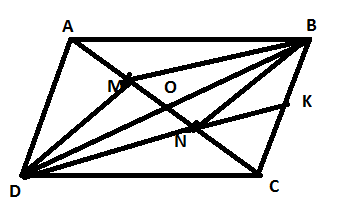
a) Xét ADM và
CBN có:
AM = CN (gt)
DAM =
BCN ( cặp góc so le trog, AD // BC)
AD = BC (ABCD là hình bình hành)
Do đó: ∆ ADM = ∆CBN (c-g-c)
=> DM = BN (1)
Xét ABM và
CDN có :
AM = CN (GT)
góc BAM = góc DCN (cặp góc so le trog, AB // DC)
AB = CD (ABCD là hình bình hành)
Do đó: ∆ ABM = ∆CDN (c-g-c)
=> BM = DN (2)
Từ (1) và (2)
=>BMDN là hình bình hành
b) OB = OD (vì BMDN là hình bình hành)
=> CO là trung tuyến của
+ format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22math1ed582716bfb4738ccd92405301%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%227.5%22%20y%3D%2216%22%3E%26%23x2206%3B%3C%2Ftext%3E%3C%2Fsvg%3E) BMC có : NK // NC
BMC có : NK // NC
N là trung điểm MC
=>K là trung điểm BC
=>DK là đg trung tuyến
+ format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22math1ed582716bfb4738ccd92405301%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%227.5%22%20y%3D%2216%22%3E%26%23x2206%3B%3C%2Ftext%3E%3C%2Fsvg%3E) BCD có : trung tuyến DK cắt tr.tuyến CO tại N
BCD có : trung tuyến DK cắt tr.tuyến CO tại N
=>N là trọng tâm của format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22math1c213877427b46fa96cff6c39e8%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%229.5%22%20y%3D%2216%22%3E%26%23x25B3%3B%3C%2Ftext%3E%3C%2Fsvg%3E) BCD
BCD
Quảng cáo
Câu hỏi hot cùng chủ đề
Gửi báo cáo thành công!












