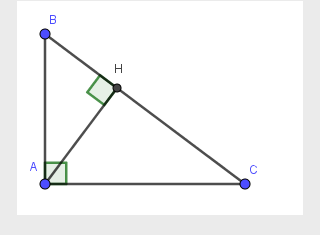
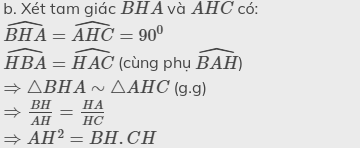Chứng minh: AB2 = BH.BC; AC2= CH.BC; AH2 = BH.CH; AH.BC=AB.AC
Quảng cáo
5 câu trả lời 7939
a.
Xét ΔABHΔABH và ΔCBAΔCBA có:
góc H bằng góc A(=90o)
góc B chung
Do đó: ΔABH∼CBAΔABH∼CBA (g-g)
⇒ABBH=BCAB⇒AB2=BC.BH⇒ABBH=BCAB⇒AB2=BC.BH ( ĐPCM)
Xét ΔABCvàΔHACΔABCvàΔHAC có:
góc A = góc H ( =90o)
góc C chung
Do đó: ΔABC∼ΔHACΔABC∼ΔHAC (g.g)
⇒ACBC=CHAC⇒AC2=BC.CH⇒ACBC=CHAC⇒AC2=BC.CH ( ĐPCM)
Ta có: ΔABH∼ΔCBAΔABH∼ΔCBA
=> góc BAH = góc ACB
Xét ΔABHΔABH và ΔCAHΔCAH
có: góc H = 90o
góc BAH = góc ACB (cmt)
Do đó: ΔABH∼ΔCAHΔABH∼ΔCAH
⇒AHHB=HCAH⇒AH2=HB.HC⇒AHHB=HCAH⇒AH2=HB.HC ( D0PCM)
d.
Ta có: ΔABH∼ΔCBAΔABH∼ΔCBA
⇒ABAH=BCAC⇒AB.AC=BC.AH⇒ABAH=BCAC⇒AB.AC=BC.AH ( ĐPCM)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191
Gửi báo cáo thành công!